题目内容
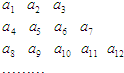 将数列{an} 中的所有项按第一排三项,以下每一行比上一行多一项的规则排成如数表:记表中的第一列数a1,a4,a8,…构成的数列为{bn},已知:
将数列{an} 中的所有项按第一排三项,以下每一行比上一行多一项的规则排成如数表:记表中的第一列数a1,a4,a8,…构成的数列为{bn},已知:①在数列{bn} 中,b1=1,对于任何n∈N*,都有(n+1)bn+1-nbn=0;
②表中每一行的数按从左到右的顺序均构成公比为q(q>0)的等比数列;
③a66=
| 2 |
| 5 |
(1)求数列{bn} 的通项公式;
(2)求上表中第k(k∈N*)行所有项的和S(k);
(3)若关于x的不等式S(k)+
| 1 |
| k |
| 1-x2 |
| x |
| 1 |
| 1000 |
| 1 |
| 100 |
分析:(1)根据题意知
=
,因此
=
,
=
,…,
=
,将各式相乘得 bn=
;
(2)设上表中每行的公比都为q,表中第1行至第9行共含有数列bn的前63项,故a66在表中第10行第三列.由此可求出上表中第k(k∈N*)行所有项的和s(k);
(3)先求
-x在x∈[
,
]上的最大值,再解不等式即可.
| bn+1 |
| bn |
| n |
| n+1 |
| b2 |
| b1 |
| 1 |
| 2 |
| b3 |
| b2 |
| 2 |
| 3 |
| bn |
| bn-1 |
| n-1 |
| n |
| 1 |
| n |
(2)设上表中每行的公比都为q,表中第1行至第9行共含有数列bn的前63项,故a66在表中第10行第三列.由此可求出上表中第k(k∈N*)行所有项的和s(k);
(3)先求
| 1 |
| x |
| 1 |
| 1000 |
| 1 |
| 100 |
解答:解:(1)由(n+1)bn+12-nbn2+bn+1bn=0,bn>0,
令 t=
得t>0,且(n+1)t2+t-n=0(6分)
即(t+1)[(n+1)t-n]=0,
所以
=
(8分)
因此
=
,
=
,…,
=
,将各式相乘得 bn=
;
(2)设上表中每行的公比都为q,且q>0.因为3+4+5+…+11=63,所以表中第1行至第9行共含有数列bn的前63项,故a66在表中第10行第三列,因此a66=b10•q2=
又b10=
所以q=2.则 S(k)=
=
(2k+2-1)k∈N*
(3)当x∈[
,
]时,∵
-x为减函数,∴最小值为100-
,∴
(2k+2-1)>100-
,∴k≥8
令 t=
| bn+1 |
| bn |
即(t+1)[(n+1)t-n]=0,
所以
| bn+1 |
| bn |
| n |
| n+1 |
因此
| b2 |
| b1 |
| 1 |
| 2 |
| b3 |
| b2 |
| 2 |
| 3 |
| bn |
| bn-1 |
| n-1 |
| n |
| 1 |
| n |
(2)设上表中每行的公比都为q,且q>0.因为3+4+5+…+11=63,所以表中第1行至第9行共含有数列bn的前63项,故a66在表中第10行第三列,因此a66=b10•q2=
| 2 |
| 5 |
| 1 |
| 10 |
| bk(1-qk+2) |
| 1-q |
| 1 |
| k |
(3)当x∈[
| 1 |
| 1000 |
| 1 |
| 100 |
| 1 |
| x |
| 1 |
| 100 |
| 1 |
| k |
| 1 |
| 100 |
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
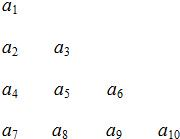 将数列{an}中的所有项按每一行比上一行多一项的规则排成如下数表:a1a2a3a4a5a6a7a8a9a10…记表中的第一列数a1,a2,a4,a7,…构成的数列为{bn},b1=a1=1.Sn为数列{bn}的前n项和,且满足
将数列{an}中的所有项按每一行比上一行多一项的规则排成如下数表:a1a2a3a4a5a6a7a8a9a10…记表中的第一列数a1,a2,a4,a7,…构成的数列为{bn},b1=a1=1.Sn为数列{bn}的前n项和,且满足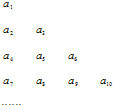 将数列{an}中的所有项按每一行比上一行多一项的规则排成如下表:
将数列{an}中的所有项按每一行比上一行多一项的规则排成如下表: