题目内容
定义:如果函数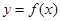 在区间
在区间 上存在
上存在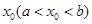 ,满足
,满足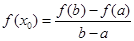 ,则称
,则称 是函数
是函数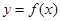 在区间
在区间 上的一个均值点。已知函数
上的一个均值点。已知函数 在区间
在区间 上存在均值点,则实数
上存在均值点,则实数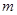 的取值范围是 .
的取值范围是 .
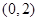 .
.
解析试题分析:由题意设函数 在区间
在区间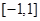 上的均值点为
上的均值点为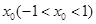 ,则
,则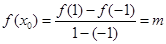 ,易知函数
,易知函数 的对称轴为
的对称轴为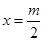 ,①当
,①当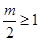 即
即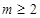 时,有
时,有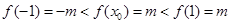 ,显然不成立,不合题意;②当
,显然不成立,不合题意;②当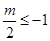 即
即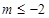 时,有
时,有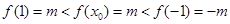 ,显然不成立,不合题意;③当
,显然不成立,不合题意;③当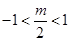 即
即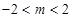 时,(1)当
时,(1)当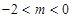 有
有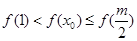 ,即
,即 ,显然不成立;(2)当
,显然不成立;(2)当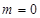 时,
时, 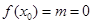 ,此时
,此时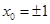 ,与
,与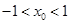 矛盾,即
矛盾,即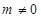 ;(3)当
;(3)当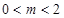 时,有
时,有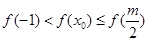 ,即
,即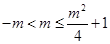 ,解得
,解得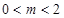 ,综上所述得实数
,综上所述得实数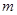 的取值范围为
的取值范围为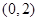 .
.
考点:二次函数的性质.

练习册系列答案
相关题目
设集合 且
且 ,
, ,对应关系
,对应关系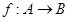 如下表(即1到26按由小到大顺序排列的自然数与按照字母表顺序排列的26个英文小写字母之间的一一对应):
如下表(即1到26按由小到大顺序排列的自然数与按照字母表顺序排列的26个英文小写字母之间的一一对应):
 | 1 | 2 | 3 | 4 | 5 | … | 25 | 26 |
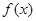 | 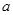 | 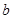 |  | 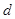 | 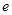 | … |  |  |
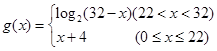 ,若
,若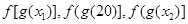 ,
,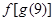 所表示的字母依次排列恰好组成的英文单词为“
所表示的字母依次排列恰好组成的英文单词为“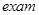 ”,则
”,则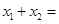 ______.
______.  且
且 ,
, ,当
,当 时均有
时均有 ,则实数
,则实数 的取值范围是 .
的取值范围是 .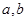 ,定义运算“
,定义运算“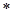 ”:
”: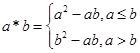 ,设
,设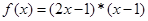 ,且关于x的方程
,且关于x的方程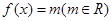 恰有三个互不相等的实数根
恰有三个互不相等的实数根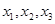 ,则
,则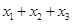 的取值范围是____________.
的取值范围是____________. 件某产品所用的时间(单位:分钟)为
件某产品所用的时间(单位:分钟)为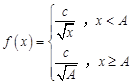 (
(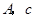 为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是 .
为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是 .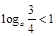 (其中
(其中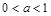 )成立的
)成立的 的取值范围是 .
的取值范围是 . 成立的实数
成立的实数 的取值范围是 .
的取值范围是 .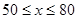 时,每天售出的件数
时,每天售出的件数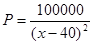 ,当销售价格定为 元时所获利润最多.
,当销售价格定为 元时所获利润最多.
 ,则
,则 .
.