题目内容
(08年潍坊市七模) 如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面![]() 内作菱形ABCD,边长为1,∠BAD=60°,再在
内作菱形ABCD,边长为1,∠BAD=60°,再在![]() 的上侧,分别以△
的上侧,分别以△![]() 与△
与△![]() 为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
(1)求证:PQ⊥BD;
(2)求二面角P-BD-Q的余弦值;
(3)求点P到平面QBD的距离;
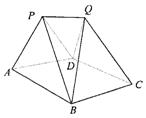
解析:(1)由P-ABD,Q-CBD是相同正三棱锥,可知△PBD与△QBD是全等等腰△.取BD中点E,连结PE、QE,则BD⊥PE,BD⊥QE.故BD⊥平面PQE,从而BD⊥PQ.
(2)由(1)知∠PEQ是二面角P-BD-Q的平面角,作PM⊥平面![]() ,垂足为M,作QN⊥平面
,垂足为M,作QN⊥平面![]() ,垂足为N,则PM∥QN,M、N分别是正△ABD与正△BCD的中心,从而点A、M、E、N、C共线,PM与QN确定平面PACQ,且PMNQ为矩形.可得ME=NE=
,垂足为N,则PM∥QN,M、N分别是正△ABD与正△BCD的中心,从而点A、M、E、N、C共线,PM与QN确定平面PACQ,且PMNQ为矩形.可得ME=NE=![]() ,PE=QE=
,PE=QE=![]() ,PQ=MN=
,PQ=MN=![]() ,∴ cos∠PEQ=
,∴ cos∠PEQ=![]() ,即二面角平面角为
,即二面角平面角为![]() .
.
(3)由(1)知BD⊥平面PEQ.设点P到平面QBD的距离为h,则
![]()
∴ ![]() .
.
∴ ![]() . ∴
. ∴ ![]() .
.

练习册系列答案
相关题目