题目内容
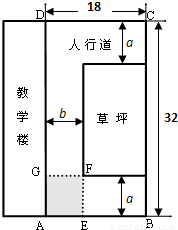
 如图所示,某学校的教学楼前有一块矩形空地ABCD,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为a米与b米(a与b均不小于2米),且要求“转角处”(图中矩形AEFG)的面积为8平方米.
如图所示,某学校的教学楼前有一块矩形空地ABCD,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为a米与b米(a与b均不小于2米),且要求“转角处”(图中矩形AEFG)的面积为8平方米.(Ⅰ)试用a表示草坪的面积S(a),并指出a的取值范围;
(Ⅱ)如何设计人行道的宽度a、b,才能使草坪的面积最大?并求出草坪的最大面积.
分析:(I)利用面积,确定a,b的关系,可得a的范围,进而可表示出草坪的面积S(a);
(II)利用基本不等式,可求最值.
(II)利用基本不等式,可求最值.
解答:解:(Ⅰ)由条件知,ab=8, ∴b=
…(1分)
∵b≥2,∴
≥2,∴2≤a≤4…(3分)
∴S(a)=(32-2a)(18-b)
即:S(a)=-4(9a+
)+592(2≤a≤4)…(6分)
(Ⅱ)∵9a+
≥2
≥48…(9分)
当9a=
,即a=
时,上式取“=”号,则S(a)≤-4×48+592=400
即a=
时,S(a)取得最大值,最大值为400.…(11分)
答:当人行道的宽度a、b分别为
米和3米时,草坪的面积达到最大,最大面积是400平方米 …(12分)
| 8 |
| a |
∵b≥2,∴
| 8 |
| a |
∴S(a)=(32-2a)(18-b)
即:S(a)=-4(9a+
| 64 |
| a |
(Ⅱ)∵9a+
| 64 |
| a |
9a•
|
当9a=
| 64 |
| a |
| 8 |
| 3 |
即a=
| 8 |
| 3 |
答:当人行道的宽度a、b分别为
| 8 |
| 3 |
点评:本题考查函数模型的构建,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 ,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为
,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为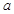 米与
米与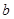 米均不小于2米,且要求“转角处”(图中矩形
米均不小于2米,且要求“转角处”(图中矩形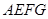 )的面积为8平方米
)的面积为8平方米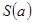 ,并指出
,并指出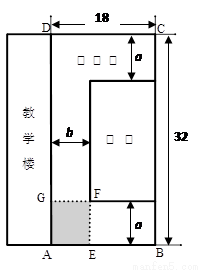
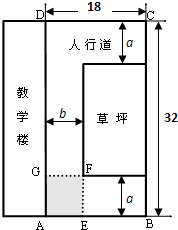 如图所示,某学校的教学楼前有一块矩形空地ABCD,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为a米与b米(a与b均不小于2米),且要求“转角处”(图中矩形AEFG)的面积为8平方米.
如图所示,某学校的教学楼前有一块矩形空地ABCD,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为a米与b米(a与b均不小于2米),且要求“转角处”(图中矩形AEFG)的面积为8平方米.