题目内容
已知函数f(x)=
,把函数g(x)=f(x)-x的零点按从小到的顺序排列成一个数列,则该数列的通项公式为 .
|
考点:分段函数的应用,数列的概念及简单表示法
专题:函数的性质及应用,等差数列与等比数列
分析:根据函数的零点的定义,构造两函数图象的交点,交点的横坐标即为函数的零点,再通过数列及通项公式的概念得所求的解.
解答: 解:当x∈(-∞,0]时,由g(x)=f(x)-x=2x-1-x=0,得2x=x+1.令y=2x,y=x+1.在同一个坐标系内作出两函数在区间(-∞,0]上的图象,由图象易知交点为(0,1),故得到函数的零点为x=0.
解:当x∈(-∞,0]时,由g(x)=f(x)-x=2x-1-x=0,得2x=x+1.令y=2x,y=x+1.在同一个坐标系内作出两函数在区间(-∞,0]上的图象,由图象易知交点为(0,1),故得到函数的零点为x=0.
当x∈(0,1]时,x-1∈(-1,0],f(x)=f(x-1)+1=2x-1-1+1=2x-1,由g(x)=f(x)-x=2x-1-x=0,得2x-1=x.令y=2x-1,y=x.在同一个坐标系内作出两函数在区间(0,1]上的图象,由图象易知交点为(1,1),故得到函数的零点为x=1.
当x∈(1,2]时,x-1∈(0,1],f(x)=f(x-1)+1=2x-1-1+1=2x-2+1,由g(x)=f(x)-x=2x-2+1-x=0,得2x-2=x-1.令y=2x-2,y=x-1.在同一个坐标系内作出两函数在区间(1,2]上的图象,由图象易知交点为(2,1),故得到函数的零点为x=2.
依此类推,当x∈(2,3],x∈(3,4],…,x∈(n,n+1]时,构造的两函数图象的交点依次为
(3,1),(4,1),…,(n+1,1),得对应的零点分别为x=3,x=4,…,x=n+1.
故所有的零点从小到大依次排列为0,1,2,…,n+1.其对应的数列的通项公式为an=n-1.
故答案为:an=n-1.
 解:当x∈(-∞,0]时,由g(x)=f(x)-x=2x-1-x=0,得2x=x+1.令y=2x,y=x+1.在同一个坐标系内作出两函数在区间(-∞,0]上的图象,由图象易知交点为(0,1),故得到函数的零点为x=0.
解:当x∈(-∞,0]时,由g(x)=f(x)-x=2x-1-x=0,得2x=x+1.令y=2x,y=x+1.在同一个坐标系内作出两函数在区间(-∞,0]上的图象,由图象易知交点为(0,1),故得到函数的零点为x=0.当x∈(0,1]时,x-1∈(-1,0],f(x)=f(x-1)+1=2x-1-1+1=2x-1,由g(x)=f(x)-x=2x-1-x=0,得2x-1=x.令y=2x-1,y=x.在同一个坐标系内作出两函数在区间(0,1]上的图象,由图象易知交点为(1,1),故得到函数的零点为x=1.
当x∈(1,2]时,x-1∈(0,1],f(x)=f(x-1)+1=2x-1-1+1=2x-2+1,由g(x)=f(x)-x=2x-2+1-x=0,得2x-2=x-1.令y=2x-2,y=x-1.在同一个坐标系内作出两函数在区间(1,2]上的图象,由图象易知交点为(2,1),故得到函数的零点为x=2.
依此类推,当x∈(2,3],x∈(3,4],…,x∈(n,n+1]时,构造的两函数图象的交点依次为
(3,1),(4,1),…,(n+1,1),得对应的零点分别为x=3,x=4,…,x=n+1.
故所有的零点从小到大依次排列为0,1,2,…,n+1.其对应的数列的通项公式为an=n-1.
故答案为:an=n-1.
点评:本题主要考查了函数零点的概念及零点的求法、数列的概念及简单表示;培养学生观察、分析、归纳、推理的能力;解题中使用了数形结合及分类讨论的数学方法和数学思想.

练习册系列答案
相关题目
若不等式lg
≥(x-1)lgn对任意不大于1的实数x和大于1的正整数n都成立,则a的取值范围是( )
| 1x+2x+…+(n-1)x+(1-a)nx |
| n |
| A、[0,+∞) | ||
| B、(-∞,0] | ||
C、[
| ||
D、(-∞,
|
已知函数f(x)=
若函数y=g(x)的图象与函数y=f-1(x-1)的图象关于直线y=x对称,则g(11)的值是( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知正四面体的俯视图如图所示,其中四边形ABCD是边长为2的正方形,则这个正四面体的主视图的面积为( )
已知正四面体的俯视图如图所示,其中四边形ABCD是边长为2的正方形,则这个正四面体的主视图的面积为( )A、2
| ||
B、
| ||
C、2
| ||
D、
|
计算机执行如图程序段后,输出的结果是( )
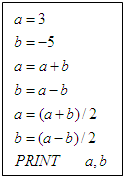
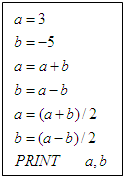
| A、0.5,-2.5 | B、3,-5 | C、0.5,-1.25 | D、-4.5,1.25 |
 上网获取信息已经成为人们日常生活的重要组成部分.因特网服务公司(Internet Service Provider)的任务就是负责将用户的计算机接入因特网,同时收取一定的费用.某同学要把自己的计算机接入因特网.现有两家ISP公司可供选择.公司A每小时收费1.5元;公司B的收费原则如图所示,即在用户上网的第1小时内收费1.7,第2小时内收费1.6元,以后每小时减少0.1元(若用户一次上网时间超过17小时,按17小时计算).假设一次上网时间总小于17小时.那么,一次上网在多长时间以内能够保证选择公司A比选择公司B所需费用少?请写出其中的不等关系.
上网获取信息已经成为人们日常生活的重要组成部分.因特网服务公司(Internet Service Provider)的任务就是负责将用户的计算机接入因特网,同时收取一定的费用.某同学要把自己的计算机接入因特网.现有两家ISP公司可供选择.公司A每小时收费1.5元;公司B的收费原则如图所示,即在用户上网的第1小时内收费1.7,第2小时内收费1.6元,以后每小时减少0.1元(若用户一次上网时间超过17小时,按17小时计算).假设一次上网时间总小于17小时.那么,一次上网在多长时间以内能够保证选择公司A比选择公司B所需费用少?请写出其中的不等关系.