题目内容
已知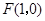 ,直线
,直线 ,
,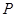 为平面上的动点,过点
为平面上的动点,过点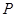 作
作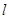 的垂线,垂足为点
的垂线,垂足为点 ,且
,且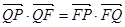 .
.
(1)求动点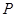 的轨迹曲线
的轨迹曲线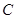 的方程;
的方程;
(2)设动直线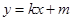 与曲线
与曲线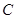 相切于点
相切于点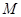 ,且与直线
,且与直线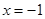 相交于点
相交于点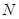 ,试探究:在坐标平面内是否存在一个定点
,试探究:在坐标平面内是否存在一个定点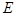 ,使得以
,使得以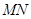 为直径的圆恒过此定点
为直径的圆恒过此定点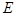 ?若存在,求出定点
?若存在,求出定点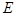 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】
(1)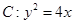 (2)存在一个定点
(2)存在一个定点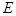
【解析】
试题分析:解:(1)设点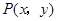 ,则
,则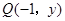 ,由
,由 ,得
,得
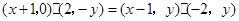 ,化简得
,化简得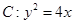 4分
4分
(2)由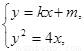 得
得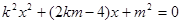 ,
,
由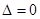 ,得
,得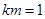 ,从而有
,从而有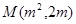 ,
,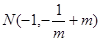 , 7分
, 7分
则以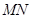 为直径的圆的方程为
为直径的圆的方程为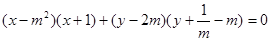 ,
,
整理得,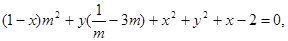 10分
10分
由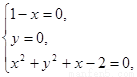 得
得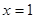 ,
,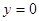
所以存在一个定点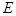
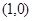 符合题意. 14分
符合题意. 14分
考点:直线与抛物线位置关系
点评:主要是考查了向量的坐标关系,以及直线与抛物线的位置关系的运用,属于中档题。

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目