题目内容
(本小题满分12分)
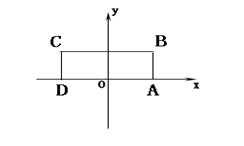如图，在矩形ABCD中，已知A（2，0）、C（－2，2），点P在BC边上移动，线段OP的垂直平分线交y轴于点E，点M满足
(Ⅰ)求点M的轨迹方程；
(Ⅱ)已知点F（0，
），过点F的直线l与点M的轨迹相交于Q、R两点，且
求实数
的取值范围.
(Ⅰ) 点M的轨迹方程为x2=－4(y－1)( 
) (Ⅱ) 
解析:
(Ⅰ)依题意，设P（t,2）（
），M（x，y）.
当t=0时，点M与点E重合，则M（0，1），
当t≠0时，线段OP的垂直平分线方程为：
…… 3分
即
由
得
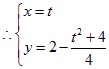
显然，点（0，1）适合上式 .
故点M的轨迹方程为x2=－4(y－1)( )… 6分
(Ⅱ)设
得x2+4kx－2=0.
设Q（x1,y1）、R（x2,y2），则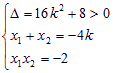
……… 8分
,
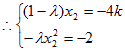.消去x2，得
.…10分
解得 12分
练习册系列答案
名校课堂系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
