题目内容
求证:当f(x)=ax2+bx+c(a≠0)时,方程ax2+bx+c=0有不等实根的充要条件是:存在x∈R使得a•f(x)<0.
【答案】分析:结合二次函数和二次方程的特点,从必要性和充分性两方面来证即可.
解答:证明:必要性:设方程ax2+bx+c=0有不等实根x1<x2,
根据韦达定理有 ,
, ,
,
取x=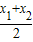 =
= ,代入函数解析式可得
,代入函数解析式可得
f(x)= =
= ,
,
因为方程有两个实根,所以b2-4ac>0,
所以a•f(x)= <0成立;
<0成立;
充分性:如果存在x使得a•f(x)<0,即a2x2+abx+ac<0在x=x处成立,
因为a2>0,根据二次函数特点,x= 处,a2x2+abx+ac 取得最小值,
处,a2x2+abx+ac 取得最小值,
为f(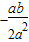 )=ac-
)=ac- ,既然它是最小值,那么f(
,既然它是最小值,那么f( )≤f(x)<0,
)≤f(x)<0,
所以ac- <0,即b2-4ac>0,故原方程必然有2个不等实根;
<0,即b2-4ac>0,故原方程必然有2个不等实根;
综上可得:方程ax2+bx+c=0有不等实根的充要条件是:存在x∈R使得a•f(x)<0.
点评:本题考查充要条件的证明,涉及一元二次方程根的分布,属基础题.
解答:证明:必要性:设方程ax2+bx+c=0有不等实根x1<x2,
根据韦达定理有
 ,
, ,
,取x=
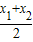 =
= ,代入函数解析式可得
,代入函数解析式可得f(x)=
 =
= ,
,因为方程有两个实根,所以b2-4ac>0,
所以a•f(x)=
 <0成立;
<0成立;充分性:如果存在x使得a•f(x)<0,即a2x2+abx+ac<0在x=x处成立,
因为a2>0,根据二次函数特点,x=
 处,a2x2+abx+ac 取得最小值,
处,a2x2+abx+ac 取得最小值,为f(
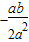 )=ac-
)=ac- ,既然它是最小值,那么f(
,既然它是最小值,那么f( )≤f(x)<0,
)≤f(x)<0,所以ac-
 <0,即b2-4ac>0,故原方程必然有2个不等实根;
<0,即b2-4ac>0,故原方程必然有2个不等实根;综上可得:方程ax2+bx+c=0有不等实根的充要条件是:存在x∈R使得a•f(x)<0.
点评:本题考查充要条件的证明,涉及一元二次方程根的分布,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目