题目内容
已知定义在R上的函数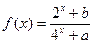 为偶函数.且
为偶函数.且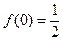
(1)求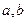 的值;
的值;
(2)判断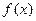 在
在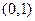 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(3)若方程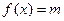 在
在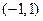 上有解,求
上有解,求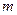 的取值范围?
的取值范围?
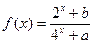 为偶函数.且
为偶函数.且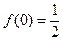
(1)求
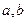 的值;
的值;(2)判断
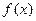 在
在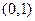 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;(3)若方程
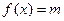 在
在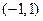 上有解,求
上有解,求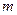 的取值范围?
的取值范围?(1) 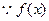 为偶函数
为偶函数 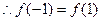 ,又
,又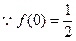
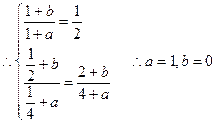
(2)证明: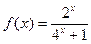 在(0,1)上是减函数
在(0,1)上是减函数
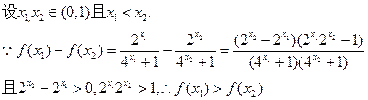
所以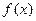 在(0,1)上是减函数 。
在(0,1)上是减函数 。
(用求导做同样给分)
(3)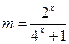
 当
当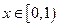 时,函数
时,函数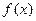 单调递减,
单调递减,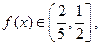
又因为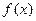 是偶函数,所以当
是偶函数,所以当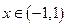 时,
时,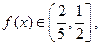
所以当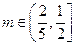 时,方程在(-1,1)上有解。
时,方程在(-1,1)上有解。
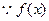 为偶函数
为偶函数 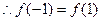 ,又
,又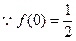
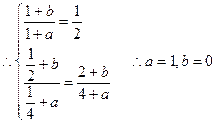
(2)证明:
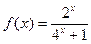 在(0,1)上是减函数
在(0,1)上是减函数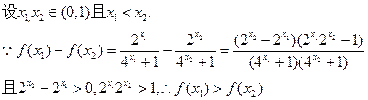
所以
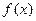 在(0,1)上是减函数 。
在(0,1)上是减函数 。 (用求导做同样给分)
(3)
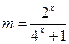
 当
当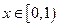 时,函数
时,函数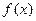 单调递减,
单调递减,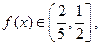
又因为
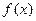 是偶函数,所以当
是偶函数,所以当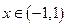 时,
时,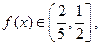
所以当
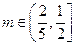 时,方程在(-1,1)上有解。
时,方程在(-1,1)上有解。略

练习册系列答案
相关题目
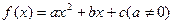 的图象过点
的图象过点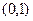 ,且与
,且与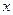 轴有唯一的交点
轴有唯一的交点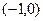 。
。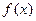 的表达式;
的表达式;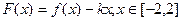 ,记此函数的最小值为
,记此函数的最小值为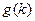 ,求
,求 )
)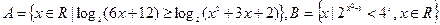 .
. (CRB )
(CRB )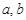 满足等式
满足等式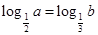 ,下列四个关系式:①
,下列四个关系式:①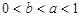 ;
;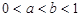 ;③
;③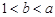 ;④
;④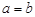 ,其中不可能成立的关系式有
,其中不可能成立的关系式有 1个
1个  2个
2个  3个
3个  4个
4个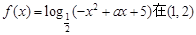 上是增函数,则
上是增函数,则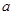 的取值范围是
的取值范围是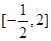



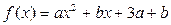 是偶函数,定义域为
是偶函数,定义域为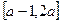 ,则
,则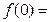
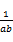 ≥4+
≥4+ =4
=4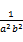 ≥( _________ );a3b3+
≥( _________ );a3b3+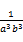 ≥( _________ );
≥( _________ );