题目内容
(本大题满分12分)
已知点A(-1,0)、B(1,0)和动点M满足:![]() ,且
,且![]() ,动点M的轨迹为曲线C,过点B的直线交C于P、Q两点.
,动点M的轨迹为曲线C,过点B的直线交C于P、Q两点.
(1)求曲线C的方程;
(2)求△APQ面积的最大值.
(1)解:设M (x,y),在△MAB中,| AB | = 2,![]()
∴![]()
即![]()
因此点M的轨迹是以A、B为焦点的椭圆,a = 2,c = 1
∴曲线C的方程为![]() .
.
(2)解法一:设直线PQ方程为![]() (
(![]() ∈R)
∈R)
由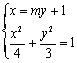 得:
得:![]()
显然,方程①的![]() ,设P(x1,y1),Q(x2,y2),则有
,设P(x1,y1),Q(x2,y2),则有![]()
![]()
![]()
令![]() ,则t≥3,
,则t≥3,
由于函数![]() 在[3,+∞)上是增函数,∴
在[3,+∞)上是增函数,∴![]()
故![]() ,即S≤3
,即S≤3
∴△APQ的最大值为3
解法二:设P(x1,y1),Q(x2,y2),则![]()
当直线PQ的斜率不存在时,易知S = 3
设直线PQ方程为![]()
由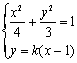 得:
得:![]() ①
①
显然,方程①的△>0,则![]()
∴![]()
![]()
![]()
令![]() ,则
,则![]() ,即S<3
,即S<3
∴△APQ的最大值为3

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案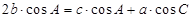 ,
,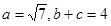 ,求△ABC的面积.
,求△ABC的面积.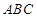 中,
中,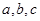 分别为内角
分别为内角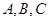 的对边,且
的对边,且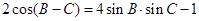
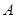
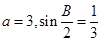 ,求
,求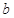
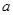 为实常数,函数
为实常数,函数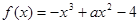 ,
,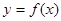 的图象在点
的图象在点 处的切线的倾斜角为
处的切线的倾斜角为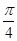 ,求函数
,求函数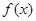 的单调区间;
的单调区间;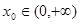 ,使
,使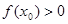 ,求
,求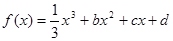 的图象过点(0,3),且在
的图象过点(0,3),且在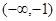 和
和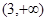 上为增
上为增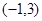 上为减函数.
上为减函数.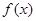 的解析式;
的解析式;