题目内容

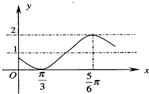精英家教网若函数f（x）=Asin（ωx+?）+B（A＞0，ω＞0，0＜?＜π）的图象如右图所示，则函数的解析式为f（x）=
 
．
分析：图象中给出了半个周期的完整图象，解出周期T，由公式求ω，又最高点与最低点的纵坐标的差为2，可得|A|=1进而求出A，b，到此函数解析式可以表示为 f（x）=sin（2x+?）+1，将点 (
π
3
，0)代入，即可求?．得到函数的解析式．
解答：解：由已知，如图
A=
1
2
(ymax-ymin)=1，
T
2
=
π
ω
=
5π
6
-
π
3
=
π
2
，ω=2．易知 b=1
∴f（x）=sin（2x+?）+1，
将点 (
π
3
，0)代入  f（x）=sin（2x+?）+1得 sin(
2π
3
+?)=-1
即
2π
3
+?=2kπ-
π
2
，k∈z解得 ?=2kπ-
7π
6
(k∈Z)
又0＜?＜π，当k=1时，?=
5π
6

∴f(x)=sin(2x+
5π
6
)+1．
故答案为：sin(2x+
5π
6
)+1．
点评：本题考点是三角函数的图象与性质，考查知道了三角函数图象上的特征求三角函数的解析式．
练习册系列答案
相关题目
设函数f（x）的定义域为R，当x＜0时f（x）＞1，且对任意的实数x，y∈R，有f（x+y）=f（x）f（y）．数列{an}满足f（an+1）=
1f(-2-an)
（n∈N*）
（Ⅰ）求f（0）的值，判断并证明函数f（x）的单调性；
（Ⅱ）如果存在t、s∈N*，s≠t，使得点（t，as）、（s，at）都在直线y=kx-1上，试判断是否存在自然数M，当n＞M时，a n＞f（0）恒成立？若存在，求出M的最小值，若不存在，请说明理由．
设函数f（x）的定义域为R，当x＜0时f（x）＞1，且对任意的实数x，y∈R，有f（x+y）=f（x）f（y）．数列{an}满足f(an+1)=
1
f(-2-an)
(n∈N*)．
（Ⅰ）求f（0）的值，判断并证明函数f（x）的单调性；
（Ⅱ）如果存在t、s∈N*，s≠t，使得点（t，as）、（s，at）都在直线y=kx-1上，试判断是否存在自然数M，当n＞M时，an＞0恒成立？若存在，求出M的最小值，若不存在，请说明理由；
（Ⅲ）若a1=f（0），不等式
1
an+1
+
1
an+2
+…+
1
a2n
＞
12
35
(1+logf(1)x)对不小于2的正整数恒成立，求x的取值范围．
设函数f（x）=
3x-1
x+1
．
（1）已知s=-t+
1
2
（t＞1），求证：f（
t-1
t
）=
s+1
s
；
（2）证明：存在函数t=φ（s）=as+b（s＞0），满足f（
s+1
s
）=
t-1
t
；
（3）设x1=
11
17
，xn+1=f（xn），n=1，2，…．问：数列{
1
xn-1
}是否为等差数列？若是，求出数列{xn}中最大项的值；若不是，请说明理由．
设函数f（x）的定义域为R，当x＜0时f（x）＞1，且对任意的实数x，y∈R，有f（x+y）=f（x）f（y）．数列{an}满足f（an+1）=（n∈N*）
（Ⅰ）求f（0）的值，判断并证明函数f（x）的单调性；
（Ⅱ）如果存在t、s∈N*，s≠t，使得点（t，as）、（s，at）都在直线y=kx-1上，试判断是否存在自然数M，当n＞M时，a n＞f（0）恒成立？若存在，求出M的最小值，若不存在，请说明理由．
设函数f（x）的定义域为R，当x＜0时f（x）＞1，且对任意的实数x，y∈R，有f（x+y）=f（x）f（y）．数列{an}满足．
（Ⅰ）求f（0）的值，判断并证明函数f（x）的单调性；
（Ⅱ）如果存在t、s∈N*，s≠t，使得点（t，as）、（s，at）都在直线y=kx-1上，试判断是否存在自然数M，当n＞M时，an＞0恒成立？若存在，求出M的最小值，若不存在，请说明理由；
（Ⅲ）若a1=f（0），不等式对不小于2的正整数恒成立，求x的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网