题目内容
【题目】已知F1 , F2是椭圆和双曲线的公共焦点,P是它们的一个公共点.且∠F1PF2= ![]() ,则椭圆和双曲线的离心率的倒数之和的最大值为( )
,则椭圆和双曲线的离心率的倒数之和的最大值为( )
A.![]()
B.![]()
C.3
D.2
【答案】A
【解析】解:设椭圆的长半轴为a,双曲线的实半轴为a1 , (a>a1),半焦距为c, 由椭圆和双曲线的定义可知,
设|PF1|=r1 , |PF2|=r2 , |F1F2|=2c,
椭圆和双曲线的离心率分别为e1 , e2
∵∠F1PF2= ![]() ,
,
∴由余弦定理可得4c2=(r1)2+(r2)2﹣2r1r2cos ![]() ,①
,①
在椭圆中,①化简为即4c2=4a2﹣3r1r2 ,
即 ![]() ,②
,②
在双曲线中,①化简为即4c2=4a12+r1r2 ,
即 ![]() ,③
,③
联立②③得, ![]() =4,
=4,
由柯西不等式得(1+ ![]() )(
)( ![]() )≥(1×
)≥(1× ![]() +
+ ![]() )2 ,
)2 ,
即( ![]() )
) ![]() =
= ![]()
即 ![]()
![]() ,d当且仅当
,d当且仅当 ![]() 时取等号,
时取等号,
法2:设椭圆的长半轴为a1 , 双曲线的实半轴为a2 , (a1>a2),半焦距为c,
由椭圆和双曲线的定义可知,
设|PF1|=r1 , |PF2|=r2 , |F1F2|=2c,
椭圆和双曲线的离心率分别为e1 , e2
∵∠F1PF2= ![]() ,
,
∴由余弦定理可得4c2=(r1)2+(r2)2﹣2r1r2cos ![]() =(r1)2+(r2)2﹣r1r2 ,
=(r1)2+(r2)2﹣r1r2 ,
由 ![]() ,得
,得 ![]() ,
,
∴ ![]() =
= ![]() ,
,
令m=  =
= 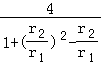 =
=  ,
,
当 ![]() 时,m
时,m ![]() ,
,
∴ ![]() ,
,
即 ![]() 的最大值为
的最大值为 ![]() ,
,
法3:设PF1|=m,|PF2|=n,则 ![]() ,
,
则a1+a2=m,
则 ![]() =
= ![]() ,
,
由正弦定理得 ![]() =
= ![]() ,
,
即 ![]() =
= ![]() sin(120°﹣θ)≤
sin(120°﹣θ)≤ ![]() =
= ![]()
故选:A
根据双曲线和椭圆的性质和关系,结合余弦定理即可得到结论.

练习册系列答案
相关题目



