题目内容
18．函数f（x）=1+2cosx的值域是[-1，3]．分析 根据cosx∈[-1，1]，求得函数f（x）=1+2cosx的值域．
解答 解：由于cosx∈[-1，1]，∴函数f（x）=1+2cosx的值域是[-1，3]，
故答案为：[-1，3]．
点评 本题主要考查余弦函数的值域，属于基础题．
练习册系列答案
相关题目
8．在平行四边形ABCD中，下列结论中错误的是（ ）
| A． | $\overrightarrow{AB}=\overrightarrow{DC}$ | B． | $\overrightarrow{AD}+\overrightarrow{AB}=\overrightarrow{AC}$ | C． | $\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{BD}$ | D． | $\overrightarrow{AD}+\overrightarrow{CD}=\overrightarrow{BD}$ |
6．已知x2+y2=4，x＞0，y＞0，且loga（2+x）=m，loga$\frac{1}{2-x}$=n，则logay等于（ ）
| A． | m+n | B． | m-n | C． | $\frac{1}{2}$（m+n） | D． | $\frac{1}{2}$（m-n） |
3．下列函数在（-∞，+∞）上为单调函数的是（ ）
| A． | y=x2-x | B． | y=|x| | C． | y=x3+2x | D． | y=sinx |
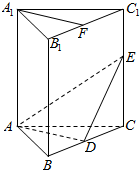如图，在直三棱柱ABC-A1B1C1中，A1B1=A1C1，F为B1C1的中点，D，E分别是棱BC，CC1上的点，且AD⊥BC．