题目内容
若（ x2-2x+3）n=a2nx2n+a2n-1x2n-1+…+a1x+a0，则a2n+a2n-2+…+a4+a2+a0=
- A.2n
- B.3n
- C.
（6n+2n） - D.（6n-2n）
C
分析：把x=1和x=-1分别代入（ x2-2x+3）n=a2nx2n+a2n-1x2n-1+…+a1x+a0，中，得出等式，再把两式相加即可．
解答：对于（ x2-2x+3）n=a2nx2n+a2n-1x2n-1+…+a1x+a0，
令x=1得2n=a2n+a2n-1+…+a1+a0，
令x=-1得6n=a2n-a2n-1+…-a1+a0，
两式相加得到2n+6n=2（a2n+a2n-2+…+a4+a2+a0），
所以a2n+a2n-2+…+a4+a2+a0=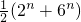
故选C．
点评：解答本题，关键是取x=±1时，奇次项系数互为相反数，可以抵消，从而得出偶次项的系数和，属于基础题．
分析：把x=1和x=-1分别代入（ x2-2x+3）n=a2nx2n+a2n-1x2n-1+…+a1x+a0，中，得出等式，再把两式相加即可．
解答：对于（ x2-2x+3）n=a2nx2n+a2n-1x2n-1+…+a1x+a0，
令x=1得2n=a2n+a2n-1+…+a1+a0，
令x=-1得6n=a2n-a2n-1+…-a1+a0，
两式相加得到2n+6n=2（a2n+a2n-2+…+a4+a2+a0），
所以a2n+a2n-2+…+a4+a2+a0=
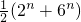
故选C．
点评：解答本题，关键是取x=±1时，奇次项系数互为相反数，可以抵消，从而得出偶次项的系数和，属于基础题．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目