题目内容
(1)设x∈R,比较x3与x2-x+1的大小.
(2)设a>0,b>0,求证: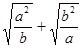 ≥
≥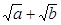 .
.
【答案】
(1)解: ∵ x3-(x2-x+1)= x3-x2+x-1=x2(x-1)+(x-1)=(x-1)(x2+1),
……………………3分
∵ x∈R,x2+1>0.
故当x>1时,(x-1)(x2+1)>0,∴ x3>x2-x+1;
当x=1时,(x-1)(x2+1)=0,∴ x3=x2-x+1;
当x<1时,(x-1)(x2+1)<0,∴ x3<x2-x+1. ……………………5分
(2)证明:∵ 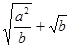 ≥
≥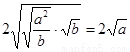 ,
,
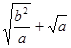 ≥
≥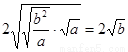 ,
……………………9分
,
……………………9分
两式相加得
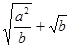 +
+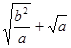 ≥
≥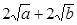 ,
,
整理得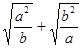 ≥
≥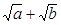 .
…………………10分
.
…………………10分
(注:该题也可用作差法证,类比给分)
【解析】略

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
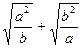 ≥
≥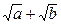 .
.