题目内容
已知双曲线的中心在原点,焦点在x轴上,离心率为2,过其右焦点且倾斜角为45°的直线被双曲线截得的弦MN的长为6.(Ⅰ)求此双曲线的方程;
(Ⅱ)若直线l:y=kx+m与该双曲线交于两个不同点A、B,且以线段AB为直径的圆过原点,求定点Q(0,-1)到直线l的距离d的最大值,并求此时直线l的方程.
【答案】分析:(1)设出双曲线的标准方程根据离心率求得a和c的关系,把直线MN的方程代入双曲线方程整理得2x2+4ax-7a2=0.设M(x1,y1),N(x2,y2),根据韦达定理表示出x1+x2和x1x2,进而用弦长公式表示出||MN|求得a,进而根据离心率求得c,进而求得b,则双曲线方程可得.
(2)直线l与双曲线法才联立消去y,设A(x3,y3),B(x4,y4),利用韦达定理表示出x3+x4和x3x4,依据以线段AB为直径的圆过原点,所以x3x4+y3y4=0.代入求得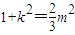 由点到直线的距离表示出d,根据k的范围确定m的范围,进而求得d的最大值,此时的直线l的方程可得.
由点到直线的距离表示出d,根据k的范围确定m的范围,进而求得d的最大值,此时的直线l的方程可得.
解答:解:(Ⅰ)设双曲线的方程是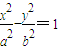 (a>0,b>0),
(a>0,b>0),
则由于离心率 ,所以c=2a,b2=3a2.
,所以c=2a,b2=3a2.
从而双曲线的方程为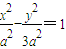 ,且其右焦点为F(2a,0).
,且其右焦点为F(2a,0).
把直线MN的方程y=x-2a代入双曲线的方程,消去y并整理,得2x2+4ax-7a2=0.
设M(x1,y1),N(x2,y2),则x1+x2=-2a, .
.
由弦长公式,得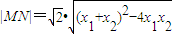 =
=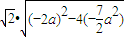 =6.
=6.
所以a=1,b2=3a2=3.
从而双曲线的方程是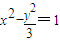 .
.
(Ⅱ)由y=kx+m和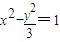 ,消去y,得(3-k2)x2-2kmx-m2-3=0.
,消去y,得(3-k2)x2-2kmx-m2-3=0.
根据条件,得△=4k2m2-4(3-k2)(-m2-3)>0且3-k2≠0.
∴m2+3>k2≠3.
设A(x3,y3),B(x4,y4),则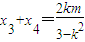 ,
,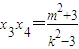 .
.
由于以线段AB为直径的圆过原点,所以x3x4+y3y4=0.
即(1+k2)x3x4+km(x3+x4)+m2=0.
从而有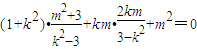 ,即
,即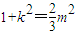 .
.
∴点Q到直线l:y=kx+m的距离为: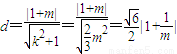 .
.
由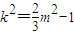 ≥0,解得
≥0,解得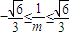 且
且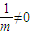 .
.
由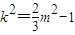 ≠3,解得
≠3,解得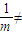
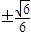 .
.
所以当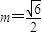 时,d取最大值
时,d取最大值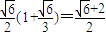 ,此时k=0.
,此时k=0.
因此d的最大值为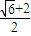 ,此时直线l的方程是
,此时直线l的方程是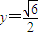 .
.
点评:本题主要考查了直线与圆锥曲线的综合问题.此类题是历年高考命题的热点,试题具有一定的综合性,覆盖面大,不仅考查“三基”掌握的情况,而且重点考查学生的作图、数形结合、等价转化、分类讨论、逻辑推理、合理运算,以及运用数学知识分析问题和解决问题的能力.
(2)直线l与双曲线法才联立消去y,设A(x3,y3),B(x4,y4),利用韦达定理表示出x3+x4和x3x4,依据以线段AB为直径的圆过原点,所以x3x4+y3y4=0.代入求得
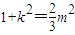 由点到直线的距离表示出d,根据k的范围确定m的范围,进而求得d的最大值,此时的直线l的方程可得.
由点到直线的距离表示出d,根据k的范围确定m的范围,进而求得d的最大值,此时的直线l的方程可得.解答:解:(Ⅰ)设双曲线的方程是
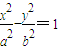 (a>0,b>0),
(a>0,b>0),则由于离心率
 ,所以c=2a,b2=3a2.
,所以c=2a,b2=3a2.从而双曲线的方程为
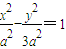 ,且其右焦点为F(2a,0).
,且其右焦点为F(2a,0).把直线MN的方程y=x-2a代入双曲线的方程,消去y并整理,得2x2+4ax-7a2=0.
设M(x1,y1),N(x2,y2),则x1+x2=-2a,
 .
.由弦长公式,得
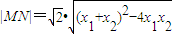 =
=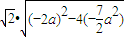 =6.
=6.所以a=1,b2=3a2=3.
从而双曲线的方程是
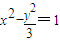 .
.(Ⅱ)由y=kx+m和
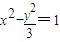 ,消去y,得(3-k2)x2-2kmx-m2-3=0.
,消去y,得(3-k2)x2-2kmx-m2-3=0.根据条件,得△=4k2m2-4(3-k2)(-m2-3)>0且3-k2≠0.
∴m2+3>k2≠3.
设A(x3,y3),B(x4,y4),则
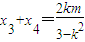 ,
,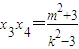 .
.由于以线段AB为直径的圆过原点,所以x3x4+y3y4=0.
即(1+k2)x3x4+km(x3+x4)+m2=0.
从而有
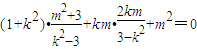 ,即
,即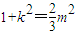 .
.∴点Q到直线l:y=kx+m的距离为:
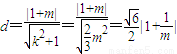 .
.由
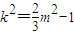 ≥0,解得
≥0,解得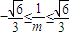 且
且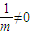 .
.由
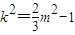 ≠3,解得
≠3,解得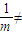
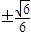 .
.所以当
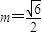 时,d取最大值
时,d取最大值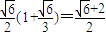 ,此时k=0.
,此时k=0.因此d的最大值为
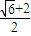 ,此时直线l的方程是
,此时直线l的方程是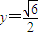 .
.点评:本题主要考查了直线与圆锥曲线的综合问题.此类题是历年高考命题的热点,试题具有一定的综合性,覆盖面大,不仅考查“三基”掌握的情况,而且重点考查学生的作图、数形结合、等价转化、分类讨论、逻辑推理、合理运算,以及运用数学知识分析问题和解决问题的能力.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目