题目内容
设函数 ,其中|t|<1,将f(x)的最小值记为g(t),则函数g(t)的单调递增区间为 .
,其中|t|<1,将f(x)的最小值记为g(t),则函数g(t)的单调递增区间为 .
【答案】分析:先利用二倍角公式对函数解析式化简整理,利用二次函数的性质和t的范围以及sin2  的范围确定函数的最小值的表达式,即g(t)进而对函数进行求导,利用导函数大于0求得t的范围,即函数g(t)的递增区间.
的范围确定函数的最小值的表达式,即g(t)进而对函数进行求导,利用导函数大于0求得t的范围,即函数g(t)的递增区间.
解答:解:f(x)=cos2x+4tsin2 +t3-3t=4sin4
+t3-3t=4sin4  +(4t-4)sin2
+(4t-4)sin2  +t3-3t+1=4(sin2
+t3-3t+1=4(sin2  +
+ )2+t3-t2-t
)2+t3-t2-t
∵|t|≤1,sin2 ≤1
≤1
∴当sin2 =-
=- 时函数有最小值为g(t)=t3-t2-t
时函数有最小值为g(t)=t3-t2-t
∴g'(t)=3t2-2t-1
当g'(t)=3t2-2t-1>0,即而|t|≤1,t<- 时,函数g(t)单调增.
时,函数g(t)单调增.
故函数g(t)的单调递增区间为:
故答案为:
点评:本题主要考查了三角函数的最值,二次函数的性质以及利用导函数判断函数单调性的问题.考查了学生综合分析问题和解决问题的能力.
 的范围确定函数的最小值的表达式,即g(t)进而对函数进行求导,利用导函数大于0求得t的范围,即函数g(t)的递增区间.
的范围确定函数的最小值的表达式,即g(t)进而对函数进行求导,利用导函数大于0求得t的范围,即函数g(t)的递增区间.解答:解:f(x)=cos2x+4tsin2
 +t3-3t=4sin4
+t3-3t=4sin4  +(4t-4)sin2
+(4t-4)sin2  +t3-3t+1=4(sin2
+t3-3t+1=4(sin2  +
+ )2+t3-t2-t
)2+t3-t2-t∵|t|≤1,sin2
 ≤1
≤1∴当sin2
 =-
=- 时函数有最小值为g(t)=t3-t2-t
时函数有最小值为g(t)=t3-t2-t∴g'(t)=3t2-2t-1
当g'(t)=3t2-2t-1>0,即而|t|≤1,t<-
 时,函数g(t)单调增.
时,函数g(t)单调增.故函数g(t)的单调递增区间为:

故答案为:

点评:本题主要考查了三角函数的最值,二次函数的性质以及利用导函数判断函数单调性的问题.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
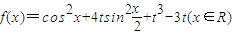 ,其中|t|<1,将f(x)的最小值记为g(t),则函数g(t)的单调递增区间为 .
,其中|t|<1,将f(x)的最小值记为g(t),则函数g(t)的单调递增区间为 . ,其中|t|≤1,将f(x)的最小值记为g(t).
,其中|t|≤1,将f(x)的最小值记为g(t).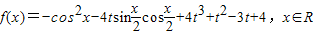 ,其中|t|≤1,将f(x)的最小值记为g(t).
,其中|t|≤1,将f(x)的最小值记为g(t). ,其中|t|≤1,将f(x)的最小值记为g(t).
,其中|t|≤1,将f(x)的最小值记为g(t).