题目内容
某中学高中学生有900名,学校要从中选出9名同学作为校庆活动的志愿者.已知高一有400名学生,高二有300名学生,高三有200名学生,为了保证每名同学都有参与的资格,学校采用分层抽样的方法抽取,若再从这9名同学中随机的抽取2人作为活动负责人,求抽到的这2名同学都是高一学生的概率分析:根据学生总数和要抽取的人数,求出三个年级要抽取的人数,其后的问题是一个古典概型,做出试验发生包含的事件是从9个人中抽取2个和满足条件的事件抽到的这2名同学都是高一学生,根据古典概型概率公式得到结果.
解答:解:∵中学高中学生有900名,
学校要从中选出9名同学作为校庆活动的志愿者,
∴每个个体被抽到的概率是
=
,
∴从高一抽400×
=4名学生,
从高二抽300×
=3名学生,
从高三抽200×
=2名学生,
由题意知本题是一个古典概型,
∵试验发生包含的事件是从9个人中抽取2个人,共有C92=36种结果,
满足条件的事件是抽到的这2名同学都是高一学生,共有C42=6
∴抽到的这2名同学都是高一学生的概率是
=
,
故答案为:
学校要从中选出9名同学作为校庆活动的志愿者,
∴每个个体被抽到的概率是
| 9 |
| 900 |
| 1 |
| 100 |
∴从高一抽400×
| 1 |
| 100 |
从高二抽300×
| 1 |
| 100 |
从高三抽200×
| 1 |
| 100 |
由题意知本题是一个古典概型,
∵试验发生包含的事件是从9个人中抽取2个人,共有C92=36种结果,
满足条件的事件是抽到的这2名同学都是高一学生,共有C42=6
∴抽到的这2名同学都是高一学生的概率是
| 6 |
| 36 |
| 1 |
| 6 |
故答案为:
| 1 |
| 6 |
点评:本题考查古典概型及其概率公式,考查分层抽样方法,考查用排列组合数表示事件数,考查利用概率知识解决实际问题,本题是一个综合题目.

练习册系列答案
相关题目
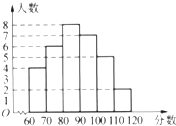 某中学部分学生参加某市高中数学竞赛,指导老师统计了所有参赛同学的成绩(成绩都为整数,试题满分120分),统计结果如图所示,请回答:
某中学部分学生参加某市高中数学竞赛,指导老师统计了所有参赛同学的成绩(成绩都为整数,试题满分120分),统计结果如图所示,请回答: