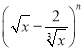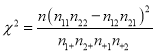题目内容
【题目】已知圆![]() 与圆
与圆![]()
![]() 的公共点的轨迹为曲线
的公共点的轨迹为曲线![]() ,且曲线
,且曲线![]() 与
与![]() 轴的正半轴相交于点
轴的正半轴相交于点![]() .若曲线
.若曲线![]() 上相异两点
上相异两点![]() 满足直线
满足直线![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求![]() 的方程;
的方程;
(2)证明直线![]() 恒过定点,并求定点的坐标.
恒过定点,并求定点的坐标.
【答案】(1)![]() ;(2)证明见解析,
;(2)证明见解析, ![]() .
.
【解析】试题分析:(1)确定![]() ,可得曲线
,可得曲线![]() 是长轴长
是长轴长![]() ,焦距
,焦距![]() 的椭圆,即可求解椭圆的方程;(2)分类讨论,设出直线的方程,代入椭圆的方程,利用韦达定理,结合直线
的椭圆,即可求解椭圆的方程;(2)分类讨论,设出直线的方程,代入椭圆的方程,利用韦达定理,结合直线![]() 的斜率之积为
的斜率之积为![]() ,即可证直线
,即可证直线![]() 恒过定点,并求出定点的坐标.
恒过定点,并求出定点的坐标.
试题解析:(1)设⊙![]() ,⊙
,⊙![]() 的公共点为
的公共点为![]() ,
,
由已知得,![]() ,
,
故![]() ,因此曲线
,因此曲线![]() 是长轴长
是长轴长![]() ,焦距
,焦距![]() 的椭圆,
的椭圆,
所以曲线![]() ;
;
(2)由曲线![]() 的方程得,上顶点
的方程得,上顶点![]() ,记
,记![]()
![]() ,
,
若直线![]() 的斜率不存在,则直线
的斜率不存在,则直线![]() 的方程为
的方程为![]() ,故
,故![]() ,且
,且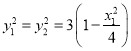 ,
,
因此![]() ,与已知不符,
,与已知不符,
因此直线AB的斜率存在,
设直线![]() ,代入椭圆
,代入椭圆![]() :
: ![]() ①
①
因为直线![]() 与曲线
与曲线![]() 有公共点
有公共点![]() ,所以方程①有两个非零不等实根
,所以方程①有两个非零不等实根![]() ,
,
故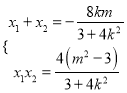 ,
,
又![]() ,
, ![]() ,
,
由![]() ,得
,得![]()
即![]()
所以![]()
化简得: ![]() ,故
,故![]() 或
或![]() ,结合
,结合![]() 知
知![]() ,
,
即直线![]() 恒过定点
恒过定点![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某中学举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出100人的成绩作为样本,对高一年级的100名学生的成绩进行统计,并按![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组,得到成绩分布的频率分布直方图(如图)。
分组,得到成绩分布的频率分布直方图(如图)。

(1)若规定60分以上(包括60分)为合格,计算高一年级这次竞赛的合格率;
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此,估计高一年级这次知识竞赛的学生的平均成绩;
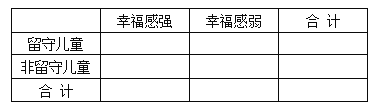
(3)若高二年级这次竞赛的合格率为![]() ,由以上统计数据填写下面
,由以上统计数据填写下面![]() 列联表,并问是否有
列联表,并问是否有![]() 的把握认为“这次知识竞赛的成绩与年级有关”。
的把握认为“这次知识竞赛的成绩与年级有关”。
高一 | 高二 | 合计 | |
合格人数 | |||
不合格人数 | |||
合计 |
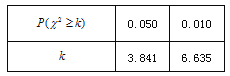
 附:参考数据与公式
附:参考数据与公式
高一 | 合计 | ||
合格人数 | a | b | a+b |
不合格人数 | c | d | c+d |
合计 | a+c | b+d | n |
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |