题目内容
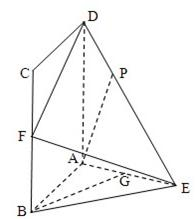 如图,平面ABCD⊥平面ABE,其中四边形ABCD是正方形,△ABE是等边三角形,且AB=2,点F、G分别是BC、AE的中点.
如图,平面ABCD⊥平面ABE,其中四边形ABCD是正方形,△ABE是等边三角形,且AB=2,点F、G分别是BC、AE的中点.(Ⅰ)求三棱锥F-ABE的体积;
(Ⅱ)求证:BG∥平面EFD;
(Ⅲ)若点P在线段DE上运动,求证:BG⊥AP.
分析:(Ⅰ)说明BF是三棱锥F-ABE的高,求出底面ABE的面积,即可求出体积;
(Ⅱ)取DE中点M,连接MG、FM,要证BG∥平面EFD,只需证明平面EFD外的直线BG,平行平面EFD内的直线FM即可.
(Ⅲ)点P在线段DE上运动,证明BG垂直平面DAE内的两条相交直线AD,AE,即可证明BG⊥平面DAE,从而证明BG⊥AP.
(Ⅱ)取DE中点M,连接MG、FM,要证BG∥平面EFD,只需证明平面EFD外的直线BG,平行平面EFD内的直线FM即可.
(Ⅲ)点P在线段DE上运动,证明BG垂直平面DAE内的两条相交直线AD,AE,即可证明BG⊥平面DAE,从而证明BG⊥AP.
解答: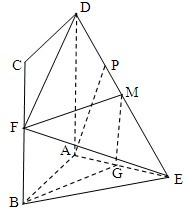 解:(Ⅰ)因为平面ABCD⊥平面ABE,且ABCD是正方形,所以BC⊥平面ABE,
解:(Ⅰ)因为平面ABCD⊥平面ABE,且ABCD是正方形,所以BC⊥平面ABE,
因为G是等边三角形ABE的边AE的中点,所以BG⊥AE,(2分)
所以VF-ABE=
S△ABE•BF=
×
AE•BG•BF=
× 2×
×1 =
.
(Ⅱ)取DE中点M,连接MG、FM,
因为MG=
AD,BF=
AD,所以MG=BF,
四边形FBGM是平行四边形,所以BG∥FM.(6分)
又因为FM?平面EFD,BG?平面EFD,
所以BG∥平面EFD.(8分)
(Ⅲ)因为DA⊥平面ABE,BG?平面ABE,所以DA⊥BG.(9分)
又BG⊥AE,AD∩AE=A,
所以BG⊥平面DAE,又AP?平面DAE,(11分)
所以BG⊥AP.(12分)
 解:(Ⅰ)因为平面ABCD⊥平面ABE,且ABCD是正方形,所以BC⊥平面ABE,
解:(Ⅰ)因为平面ABCD⊥平面ABE,且ABCD是正方形,所以BC⊥平面ABE,因为G是等边三角形ABE的边AE的中点,所以BG⊥AE,(2分)
所以VF-ABE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 3 |
| ||
| 3 |
(Ⅱ)取DE中点M,连接MG、FM,
因为MG=
| 1 |
| 2 |
| 1 |
| 2 |
四边形FBGM是平行四边形,所以BG∥FM.(6分)
又因为FM?平面EFD,BG?平面EFD,
所以BG∥平面EFD.(8分)
(Ⅲ)因为DA⊥平面ABE,BG?平面ABE,所以DA⊥BG.(9分)
又BG⊥AE,AD∩AE=A,
所以BG⊥平面DAE,又AP?平面DAE,(11分)
所以BG⊥AP.(12分)
点评:本题主要考查直线与平面的位置关系,考查空间想像能力,推理论证能力和运算求解能力.

练习册系列答案
相关题目
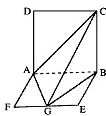 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF= 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且 (2010•河东区一模)如图,平面ABCD⊥平面ABEF,ABCD是正方形.ABEF是矩形,G是线段EF的中点,且B点在平面ACG内的射影在CG上.
(2010•河东区一模)如图,平面ABCD⊥平面ABEF,ABCD是正方形.ABEF是矩形,G是线段EF的中点,且B点在平面ACG内的射影在CG上.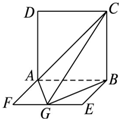 如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=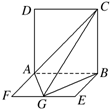 如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=