题目内容
函数f(x)=ax3+(a-1)x2+48(b-3)x+b的图象关于原点成中心对称,则f(x)
- A.在
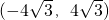 上为增函数
上为增函数 - B.在
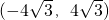 上不是单调函数
上不是单调函数 - C.在
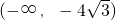 上为减函数,在
上为减函数,在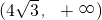 上为增函数
上为增函数 - D.在
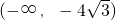 为增函数,在
为增函数,在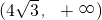 也为增函数
也为增函数
D
分析:由题意判断出f(x)必为奇函数,由此根据奇函数的定义列出方程组,进而求出函数的解析式,求出导函数后,分析导函数在各个区间上的符号,即可得到答案.
解答:由f(x)关于原点中心对称,即f(x)是奇函数,
∴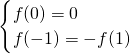 ,解得a=1,b=0,
,解得a=1,b=0,
则f(x)=x3-144x
∴f′(x)=3x2-144=3(x2-48)=3(x- )(x+
)(x+ ),
),
令f′(x)>0,则x<- 或x>
或x>
令f′(x)<0,则- <x<
<x< ,
,
∴f(x)在(- ,
, )上为减函数,在(-∞,-
)上为减函数,在(-∞,- ),(
),( ,+∞)上是增函数,
,+∞)上是增函数,
故选D.
点评:本题考查了利用导数研究函数的单调性,及函数奇偶性的性质,其中根据已知条件判断出函数为奇函数,进而求出函数的解析式,是解答本题的关键.
分析:由题意判断出f(x)必为奇函数,由此根据奇函数的定义列出方程组,进而求出函数的解析式,求出导函数后,分析导函数在各个区间上的符号,即可得到答案.
解答:由f(x)关于原点中心对称,即f(x)是奇函数,
∴
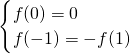 ,解得a=1,b=0,
,解得a=1,b=0,则f(x)=x3-144x
∴f′(x)=3x2-144=3(x2-48)=3(x-
 )(x+
)(x+ ),
),令f′(x)>0,则x<-
 或x>
或x>
令f′(x)<0,则-
 <x<
<x< ,
,∴f(x)在(-
 ,
, )上为减函数,在(-∞,-
)上为减函数,在(-∞,- ),(
),( ,+∞)上是增函数,
,+∞)上是增函数,故选D.
点评:本题考查了利用导数研究函数的单调性,及函数奇偶性的性质,其中根据已知条件判断出函数为奇函数,进而求出函数的解析式,是解答本题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目