题目内容
5.计算:$\frac{1}{1×3}+\frac{1}{3×5}+\frac{1}{5×7}+…+\frac{1}{2015×2017}$.分析 直接利用裂项法化简求解即可.
解答 解:$\frac{1}{1×3}+\frac{1}{3×5}+\frac{1}{5×7}+…+\frac{1}{2015×2017}$
=$\frac{1}{2}$($1-\frac{1}{3}$$+\frac{1}{3}-\frac{1}{5}$$+\frac{1}{5}-\frac{1}{7}$$+…+\frac{1}{2015}-\frac{1}{2017}$)
=$\frac{1}{2}-\frac{1}{4034}$
=$\frac{1008}{2017}$.
点评 本题考查数列求和的方法,裂项消项法的应用,考查计算能力.

练习册系列答案
相关题目
17.函数y=$\frac{1}{1-\frac{1}{x}}$的定义域是( )
| A. | {x|x∈R且x≠0} | B. | {x|x∈R且x≠1} | C. | {x|x∈R且x≠0且x≠1} | D. | {x|x∈R且x≠0或x≠1} |
14.若关于x的二次不等式ax2+bx+c≥0(a≠0)的解集是R,那么( )
| A. | a<0,且b2-4ac>0 | B. | a<0,且b2-4ac≤0 | C. | a>0,且b2-4ac≤0 | D. | a<0,且b2-4ac>0 |
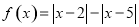 .
.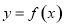 的值域;
的值域; 的解集.
的解集.