题目内容
7、已知p:|x+1|>2,q:x>a,且¬p是¬q的充分不必要条件,则实数a的取值范围可以是( )
分析:因为“若¬p则¬q”的等价命题是“若q则p”,所以q是p的充分不必要条件,即q是p的真子集,然后解不等式|x+1|>2,利用数轴求解即可.
解答:解:由题意知:
p:|x+1|>2可化简为{x|x<-3或x>1};q:x>a
∵“若¬p则¬q”的等价命题是“若q则p”,
∴q是p的充分不必要条件,即q?p
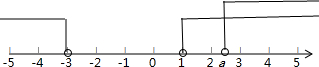
∴a≥1
故选A
p:|x+1|>2可化简为{x|x<-3或x>1};q:x>a
∵“若¬p则¬q”的等价命题是“若q则p”,
∴q是p的充分不必要条件,即q?p

∴a≥1
故选A
点评:本题主要考查四种命题的等价关系,及解绝对值不等式,属基础知识、运算能力的考查.

练习册系列答案
相关题目