Question

8．已知单位正方形的四个顶点A（0，0），B（1，0），C（1，1）和D（0，1），从A点向边CD上的点P（$\frac{3}{4}$，1）发出一束光线，这束光线被正方形各边反射（入射角等于反射角），直到经过正方形某个顶点后射出，则这束光线在正方形内经过的路程长度为5．

Answer 1

分析 由题意，画出图形，根据入射光线和反射光线的对称性以及正方形的性质得到I，J的坐标，利用两点之间的距离公式可得．

解答 解：从A点向边CD上的点P（$\frac{3}{4}$，1）发出一束光线，经过各边发射后最后由B点射出，如图，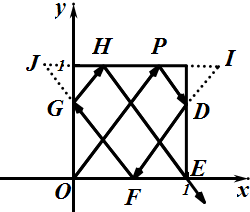
因为已知是单位正方形，这束光线在正方形内经过的路程如图，
由对称性可以得到OP=FI=HE=FJ=$\frac{5}{4}$，
所以这束光线在正方形内经过的路程的长度为$\frac{5}{4}×4$=5；
故答案为：5．

点评 本题考查了点关于直线的对称以及两点之间的距离公式的运用；关键是画出图形．