题目内容
过曲线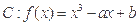 外的点
外的点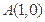 作曲线
作曲线 的切线恰有两条,
的切线恰有两条,
(1)求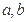 满足的等量关系;
满足的等量关系;
(2)若存在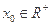 ,使
,使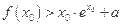 成立,求
成立,求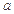 的取值范围.
的取值范围.
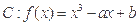 外的点
外的点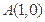 作曲线
作曲线 的切线恰有两条,
的切线恰有两条,(1)求
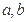 满足的等量关系;
满足的等量关系;(2)若存在
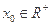 ,使
,使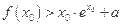 成立,求
成立,求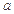 的取值范围.
的取值范围.(Ⅰ) ,
,
过点A(1,0)作曲线C的切线,设切点 ,则切线方程为:
,则切线方程为:
将 代入得:
代入得:
即 (*) 由条件切线恰有两条,方程(*)恰有两根。
(*) 由条件切线恰有两条,方程(*)恰有两根。
令 ,
, ,显然有两个极值点x=0与x=1,
,显然有两个极值点x=0与x=1,
于是 或
或
当 时,
时, ;
;
当 时,
时, ,此时
,此时 经过(1,0)与条件不符
经过(1,0)与条件不符
所以
(Ⅱ)因为存在 ,使
,使 ,即
,即
所以存在 ,使
,使 ,得
,得 ,即
,即 成立
成立
设 ,问题转化为
,问题转化为 的最大值
的最大值
 ,
,
 ,令
,令 得
得 ,
,
当 时
时 此时
此时 为增函数,当
为增函数,当 时
时 ,此时
,此时 为减函数,
为减函数,
所以 的最大值为
的最大值为

 ,
,
 的最大值
的最大值 ,得
,得
所以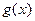 在
在 上单调递减,
上单调递减,
因此 。
。
 ,
,过点A(1,0)作曲线C的切线,设切点
 ,则切线方程为:
,则切线方程为:
将
 代入得:
代入得:
即
 (*) 由条件切线恰有两条,方程(*)恰有两根。
(*) 由条件切线恰有两条,方程(*)恰有两根。令
 ,
, ,显然有两个极值点x=0与x=1,
,显然有两个极值点x=0与x=1,于是
 或
或
当
 时,
时, ;
;当
 时,
时, ,此时
,此时 经过(1,0)与条件不符
经过(1,0)与条件不符所以

(Ⅱ)因为存在
 ,使
,使 ,即
,即
所以存在
 ,使
,使 ,得
,得 ,即
,即 成立
成立设
 ,问题转化为
,问题转化为 的最大值
的最大值 ,
, ,令
,令 得
得 ,
,当
 时
时 此时
此时 为增函数,当
为增函数,当 时
时 ,此时
,此时 为减函数,
为减函数,所以
 的最大值为
的最大值为

 ,
,
 的最大值
的最大值 ,得
,得
所以
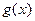 在
在 上单调递减,
上单调递减,
因此
 。
。 略

练习册系列答案
相关题目
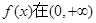 上的解析式是
上的解析式是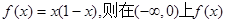 的函数解析式是( )
的函数解析式是( )



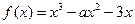
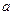 =2时,求
=2时,求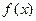 的零点;
的零点;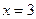 是
是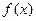 的极值点,求
的极值点,求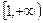 上是增函数,求实数
上是增函数,求实数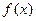 的定义域是R,对于任意实数
的定义域是R,对于任意实数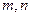 ,恒有
,恒有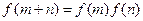 ,且当
,且当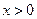 时,
时,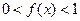 。
。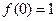 ,且当
,且当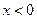 时,有
时,有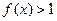 ;
;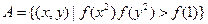 ,集合
,集合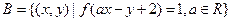 ,若A∩B=
,若A∩B= ,求a的取值范围。
,求a的取值范围。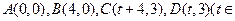 R)。记
R)。记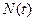 为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则
为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则 ;
; 的定义域为R,则实数k的取值范围是( )
的定义域为R,则实数k的取值范围是( )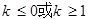



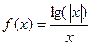 的图象可能是
的图象可能是 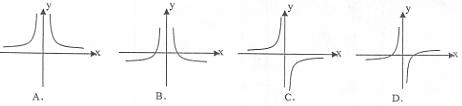
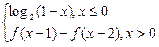 ,则f(2012)的值为( )
,则f(2012)的值为( ) 为奇函数,
为奇函数,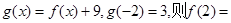 .
.