题目内容
已知直线y=2x上一点P的横坐标为a，有两个点A（-1，1），B（3，3），那么使向量
与
夹角为钝角的一个充分不必要条件是（ ）
| PA |
| PB |
| A．-1＜a＜2 | B．0＜a＜1 | C．-
| D．0＜a＜2 |
由题意知P（a，2a），向量
与
夹角为钝角的充要条件是：
•
＜0，且
•
≠-|PA|•|PB|，
即 （-1-a，1-2a）•（3-a，3-2a）＜0，
且（-1-a，1-2a）•（3-a，3-2a）≠-
•
，
解得：0＜a＜1或1＜a＜2，
故选B．
| PA |
| PB |
| PA |
| PB |
| PA |
| PB |
即 （-1-a，1-2a）•（3-a，3-2a）＜0，
且（-1-a，1-2a）•（3-a，3-2a）≠-
| (-1-a)2+(1-2a)2 |
| (3-a)2+(3-2a)2 |
解得：0＜a＜1或1＜a＜2，
故选B．
练习册系列答案
三新快车金牌周周练系列答案
相关题目
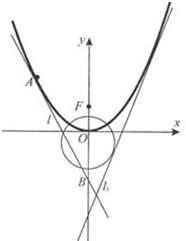如图，已知直线