题目内容
在平面上，我们如果用一条直线去截正方形的一个角，那么截下的一个直角三角形，按图所标边长，由勾股定理有：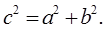
设想正方形换成正方体，把截线换成如图的截面，这时从正方体上截下三条侧棱两两垂直的三棱锥O—LMN，如果用
表示三个侧面面积，
表示截面面积，那么你类比得到的结论是（ ）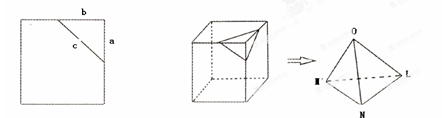
A． | B． |
C． | D． |
B
解析试题分析：建立从平面图形到空间图形的类比，于是作出猜想：S42=S12+S22+S32
故答案为：S42=S12+S22+S32.选B.
考点：类比推理
点评：本题主要考查学生的知识量和知识迁移、类比的基本能力.
练习册系列答案
相关题目
数学归纳法适用于证明的命题类型是
A．已知 结论 | B．结论已知 | C．直接证明比较困难 | D．与正整数有关 |
观察下列各式：
=3125，
=15625，
=78125， ，则
的末四位数字为（ ）
| A．3125 | B．5625 | C．0625 | D．8125 |
用反证法证明某命题时，对其结论：“自然数
中恰有一个偶数”正确的反设为（ ）
| A．都是奇数 |
| B．都是偶数 |
| C．中至少有两个偶数 |
| D．中至少有两个偶数或都是奇数 |
有一段演绎推理是这样的，“有些有理数是分数，整数是有理数，则整数是分数”，结论显然是错误的，因为
| A．大前提错误 | B．小前提错误 | C．推理形式错误 | D．非以上错误 |
把1,3,6,10,15,21，…这些数叫做三角形数，这是因为这些数目的点子可以排成一个正三角形，则第七个三角形数是( )
| A．21 | B．28 | C．32 | D．36 |
，则得分点C的坐标公式
，对于函数
上任意两点
，
，线段AB必在弧AB上方．由图象中的点C在点C′正上方，有不等式
成立．对于函数
的图象上任意两点
，
，类比上述不等式可以得到的不等式是_________ ．
内植树，第一棵
某个命题与正整数有关，如果当n＝k(k∈N＋)时，该命题成立，那么可
推得当n＝k＋1时命题也成立．现在已知当n＝5时，该命题不成立，那么可推得( )．
| A．当n＝6时该命题不成立 |
| B．当n＝6时该命题成立 |
| C．当n＝4时该命题不成立 |
| D．当n＝4时该命题成立 |