题目内容
已知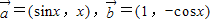 ,
,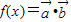 且x∈(0,2π),记f(x)在(0,2π)内零点为x.
且x∈(0,2π),记f(x)在(0,2π)内零点为x.(1)求当f(x)取得极大值时,
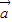 与
与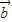 的夹角θ.
的夹角θ.(2)求f(x)>0的解集.
(3)求当函数
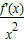 取得最小值时f(x)的值,并指出向量
取得最小值时f(x)的值,并指出向量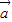 与
与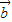 的位置关系.
的位置关系.
【答案】分析:(1)由题设知f(x)=sinx-xcosx,x∈(0,2π),故f′(x)=cosx-(cosx-xsinx)=xsinx,由此能求出当f(x)取得极大值时,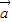 与
与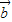 的夹角θ.
的夹角θ.
(2)由x=π是f(x)在(0,2π)内的极大值点,知f(0)=0,f(π)=π,f(2π)=-2π.由此能求出f(x)>0的解集.
(3)构造函数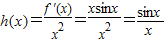 ,则
,则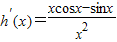 =
=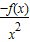 ,由此能求出当函数
,由此能求出当函数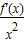 取得最小值时f(x)的值和此时向量
取得最小值时f(x)的值和此时向量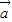 与
与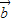 的位置关系.
的位置关系.
解答:(本题满分14分)
解:(1)∵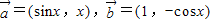 ,
,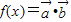 且x∈(0,2π),
且x∈(0,2π),
∴f(x)=sinx-xcosx,x∈(0,2π),
∴f′(x)=cosx-(cosx-xsinx)=xsinx,
由f′(x)=0,x∈(0,2π),得x=π,
∴x∈(0,π),f'(x)>0,则f(x)单调递增;
当x∈(π,2π),f'(x)<0,则f(x)单调递减.
∴x=π是f(x)在(0,2π)内的极大值点.…(4分)
此时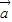 =(sinπ,π)=(0,π),
=(sinπ,π)=(0,π),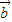 =(1,-cosπ)=(1,1)
=(1,-cosπ)=(1,1)
∴cosθ=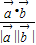 =
=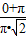 =
=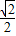 ,
,
∵0≤θ≤π,∴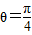 .…(6分)
.…(6分)
(2)由(1)知x=π是f(x)在(0,2π)内的极大值点.
且f(0)=0,f(π)=π,f(2π)=-2π.
∴x∈(0,π)时,f(x)>0,且f(π)•f(2π)<0,
得x∈(π,2π),
∴x∈(0,x)时,f(x)>0,即f(x)>0的解集为(0,x).…(9分)
(3)令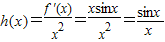 ,
,
∵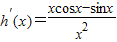 =
=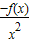 ,
,
∴h′(x)=0,得x=x,
∴x∈(0,x),f(x)>0,得h′(x)<0,则h(x)单调递减,
当x∈(x,2π),f(x)<0,得h′(x)>0,则h(x)单调递增,
∴x=x是h(x)在(0,2π)内的极小值,且h(x)为唯一极值,即为最小值,
此时f(x)=f(x)=0,即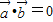 ,
,
∴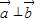 .
.
点评:本题考查向量夹角的大小的求法,考查不等式的解法,考查最小值的求法和向量位置关系的判断,综合性强,难度大,解题时要认真审题,仔细解答,注意构造法的合理运用.
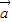 与
与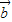 的夹角θ.
的夹角θ.(2)由x=π是f(x)在(0,2π)内的极大值点,知f(0)=0,f(π)=π,f(2π)=-2π.由此能求出f(x)>0的解集.
(3)构造函数
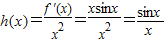 ,则
,则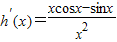 =
=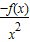 ,由此能求出当函数
,由此能求出当函数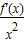 取得最小值时f(x)的值和此时向量
取得最小值时f(x)的值和此时向量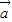 与
与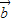 的位置关系.
的位置关系.解答:(本题满分14分)
解:(1)∵
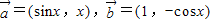 ,
,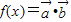 且x∈(0,2π),
且x∈(0,2π),∴f(x)=sinx-xcosx,x∈(0,2π),
∴f′(x)=cosx-(cosx-xsinx)=xsinx,
由f′(x)=0,x∈(0,2π),得x=π,
∴x∈(0,π),f'(x)>0,则f(x)单调递增;
当x∈(π,2π),f'(x)<0,则f(x)单调递减.
∴x=π是f(x)在(0,2π)内的极大值点.…(4分)
此时
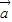 =(sinπ,π)=(0,π),
=(sinπ,π)=(0,π),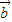 =(1,-cosπ)=(1,1)
=(1,-cosπ)=(1,1)∴cosθ=
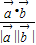 =
=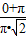 =
=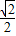 ,
,∵0≤θ≤π,∴
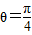 .…(6分)
.…(6分)(2)由(1)知x=π是f(x)在(0,2π)内的极大值点.
且f(0)=0,f(π)=π,f(2π)=-2π.
∴x∈(0,π)时,f(x)>0,且f(π)•f(2π)<0,
得x∈(π,2π),
∴x∈(0,x)时,f(x)>0,即f(x)>0的解集为(0,x).…(9分)
(3)令
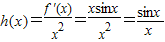 ,
,∵
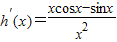 =
=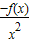 ,
,∴h′(x)=0,得x=x,
∴x∈(0,x),f(x)>0,得h′(x)<0,则h(x)单调递减,
当x∈(x,2π),f(x)<0,得h′(x)>0,则h(x)单调递增,
∴x=x是h(x)在(0,2π)内的极小值,且h(x)为唯一极值,即为最小值,
此时f(x)=f(x)=0,即
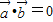 ,
,∴
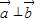 .
.点评:本题考查向量夹角的大小的求法,考查不等式的解法,考查最小值的求法和向量位置关系的判断,综合性强,难度大,解题时要认真审题,仔细解答,注意构造法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
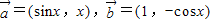 ,
,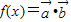 且x∈(0,2π),记f(x)在(0,2π)内零点为x.
且x∈(0,2π),记f(x)在(0,2π)内零点为x.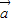 与
与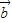 的夹角θ.
的夹角θ.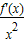 取得最小值时f(x)的值,并指出向量
取得最小值时f(x)的值,并指出向量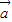 与
与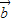 的位置关系.
的位置关系.