题目内容
在(0,2π)内,使sinx≥|cosx|成立的x的取值范围为( )
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
分析:由x在(0,2π)范围内,在平面直角坐标系中画出y=sinx和y=|cosx|的图象,根据图象可知在图中阴影部分取x的值时,sinx大于等于|cosx|,且x属于0到π,故在(0,π)范围内,求出sinx=|cosx|的x的值,根据x的值写出满足题意x的范围即可.
解答: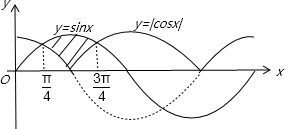
解:在(0,2π)内,画出y=sinx及y=|cosx|的图象,
由函数的图象可知,阴影部分的sixn≥|cosx|,
所以在(0,π)内,令sinx=cosx或sinx=-cosx,
而sin2x+cos2x=1,则sinx=cosx=
或sinx=-cosx=
,
解得:x=
或x=
,
则满足题意的x的取值范围为[
,
].
故选A

解:在(0,2π)内,画出y=sinx及y=|cosx|的图象,
由函数的图象可知,阴影部分的sixn≥|cosx|,
所以在(0,π)内,令sinx=cosx或sinx=-cosx,
而sin2x+cos2x=1,则sinx=cosx=
| ||
| 2 |
| ||
| 2 |
解得:x=
| π |
| 4 |
| 3π |
| 4 |
则满足题意的x的取值范围为[
| π |
| 4 |
| 3π |
| 4 |
故选A
点评:此题考查学生灵活运用同角三角函数间的基本关系化简求值,掌握正弦、余弦函数的图象与性质,考查了数形结合的数学思想,是一道基础题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
在(0,2π)内,使sinx>cosx成立的x的取值范围是( )
A、(
| ||||||
B、(
| ||||||
C、(
| ||||||
D、(
|
在(0,2π)内,使cosx>sinx>tanx成立的x的取值范围是( )
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|