题目内容

在（0，2π）内，使sinx＞cosx成立的x的取值范围是
 
．
分析：根据题意在一个坐标系中画出y=sinx、y=cosx在（0，2π）内的函数图象，由图求出不等式的解集．
解答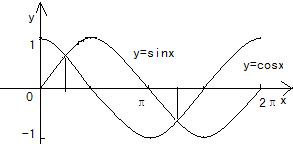：精英家教网解：在一个坐标系中画出y=sinx、y=cosx在（0，2π）内的函数图象，
由图得，在（0，2π）内，
使sinx＞cosx成立的x的取值范围是(
π
4
，
5π
4
)，
故答案为：(
π
4
，
5π
4
)．
点评：本题考查了三角函数不等式的解法，即画出正弦（余弦）函数的图象，根据图象求出不等式的解集，考查了数形结合思想和作图能力．
练习册系列答案
相关题目
在（0，2π）内，使sinx＞cosx成立的x的取值范围是（　　）
A、（
π 
4
，
π
2
）∪（π，
5π
4
）
B、（
π
4
，π）
C、（
π
4
，
5π
4
）
D、（
π
4
，π）∪（
5π
4
，
3π
2
）
在（0，2π）内，使cosx＞sinx＞tanx成立的x的取值范围是（　　）
A、(
π
4
，
3π
4
)
B、(
5π
4
，
3π
2
)
C、(
3π
2
，2π)
D、(
3π
2
，
7π
4
)
在（0，2π）内，使cosx＞sinx＞tanx的成立的x的取值范围是
（
3π
2
，2π）
（
3π
2
，2π）
．
在（0，2π）内，使sinx≥|cosx|成立的x的取值范围为
[
π
4
，
3π
4
]
[
π
4
，
3π
4
]
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网