题目内容
14、下列命题中:
①若函数f(x)的定义域为R,则g(x)=f(x)+f(-x)一定是偶函数;
②若f(x)是定义域为R的奇函数,对于任意的x∈R都有f(x)+f(2-x)=0,则函数f(x)的图象关于直线x=1对称;
③已知x1,x2是函数f(x)定义域内的两个值,且x1<x2,若f(x1)>f(x2),则f(x)是减函数;
④若f (x)是定义在R上的奇函数,且f (x+2)也为奇函数,则f (x)是以4为周期的周期函数.
其中正确的命题序号是
①若函数f(x)的定义域为R,则g(x)=f(x)+f(-x)一定是偶函数;
②若f(x)是定义域为R的奇函数,对于任意的x∈R都有f(x)+f(2-x)=0,则函数f(x)的图象关于直线x=1对称;
③已知x1,x2是函数f(x)定义域内的两个值,且x1<x2,若f(x1)>f(x2),则f(x)是减函数;
④若f (x)是定义在R上的奇函数,且f (x+2)也为奇函数,则f (x)是以4为周期的周期函数.
其中正确的命题序号是
①④
.分析:由偶函数的定义,可判断①的真假;由函数对称性满足的条件,及函数周期性的性质,可以判断②的真假;由减函数的定义,可判断③的真假;由周期函数的定义及性质,可以判断④的真假,进而得到答案.
解答:解:∵g(x)=f(x)+f(-x),∴g(-x)=f(-x)+f(x)=g(x),故①g(x)是偶函数为真命题,
∵定义域为R的奇函数f(x),对于任意的x∈R都有f(x)+f(2-x)=0,则f(x)=f(x-2),它表示函数是一个周期为2的周期函数,其图象不一定是轴对称图形,故②函数f(x)的图象关于直线x=1对称为假命题;
若f(x)是减函数,则要求任意x1<x2,均有f(x1)>f(x2),由于③中x1,x2是函数f(x)定义域内的两个值,不具有任意性,故③为假命题;
若f (x)是定义在R上的奇函数,且f (x+2)也为奇函数,则f (x)是以4为周期的周期函数,故④为真命题.
故答案为:①④
∵定义域为R的奇函数f(x),对于任意的x∈R都有f(x)+f(2-x)=0,则f(x)=f(x-2),它表示函数是一个周期为2的周期函数,其图象不一定是轴对称图形,故②函数f(x)的图象关于直线x=1对称为假命题;
若f(x)是减函数,则要求任意x1<x2,均有f(x1)>f(x2),由于③中x1,x2是函数f(x)定义域内的两个值,不具有任意性,故③为假命题;
若f (x)是定义在R上的奇函数,且f (x+2)也为奇函数,则f (x)是以4为周期的周期函数,故④为真命题.
故答案为:①④
点评:本题考查的知识点是命题的真假判断与应用,函数单调性的判断与证明,函数奇偶性的判断,函数图象的对称性,及函数的奇偶性,是函数性质的综合应用,熟练掌握函数性质的判定法则及函数性质的定义是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 满足
满足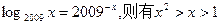 成立;
成立; 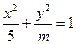 的离心率
的离心率 ,则
,则 的值为3;
的值为3; 若
若 则函数在
则函数在 内至多有一零点;
内至多有一零点; 与
与 的图像关于直线
的图像关于直线 对称;
对称; .
.