Question

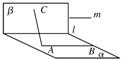12、已知平面α⊥平面β，α∩β=l，点A∈α，A∉l，直线AB∥l，直线AC⊥l，直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是（　　）

A、AB∥m

B、AC⊥m

C、AB∥β

D、AC⊥β

Answer 1

分析：利用图形可得AB∥l∥m；A对
再由AC⊥l，m∥l?AC⊥m；B对
又AB∥l?AB∥β，C对
AC⊥l，但AC不一定在平面α内，故它可以与平面β相交、平行，故不一定垂直，所以D不一定成立．

解答：解：如图所示AB∥l∥m；A对
AC⊥l，m∥l?AC⊥m；B对
AB∥l?AB∥β，C对
对于D，虽然AC⊥l，但AC不一定在平面α内，故它可以与平面β相交、平行，故不一定垂直；故错．
故选D．

点评：高考考点：线面平行、线面垂直的有关知识及应用
易错点：对有关定理理解不到位而出错．
全品备考提示：线面平行、线面垂直的判断及应用仍然是立体几何的一个重点，要重点掌握