题目内容
已知函数f(x)=alnx+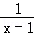 (a≠0)在(0,
(a≠0)在(0, )内有极值.
)内有极值.
(I)求实数a的取值范围;
(II)若x1∈(0, ),x2∈(2,+∞)且a∈[
),x2∈(2,+∞)且a∈[ ,2]时,求证:f(x1)﹣f(x2)≥ln2+
,2]时,求证:f(x1)﹣f(x2)≥ln2+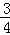 .
.
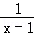 (a≠0)在(0,
(a≠0)在(0, )内有极值.
)内有极值.(I)求实数a的取值范围;
(II)若x1∈(0,
 ),x2∈(2,+∞)且a∈[
),x2∈(2,+∞)且a∈[ ,2]时,求证:f(x1)﹣f(x2)≥ln2+
,2]时,求证:f(x1)﹣f(x2)≥ln2+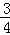 .
.(1)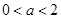 ;(2)证明过程详见解析.
;(2)证明过程详见解析.
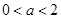 ;(2)证明过程详见解析.
;(2)证明过程详见解析.试题分析:本题主要考查导数的运算,利用导数研究函数的单调性及最值、不等式等基础知识,考查函数思想,突出考查综合运用数学知识和方法分析问题解决问题的能力.第一问,先对
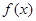 求导,由函数
求导,由函数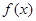 定义域可知,
定义域可知,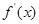 的分母为正数,设
的分母为正数,设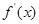 的分子为新函数
的分子为新函数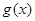 ,判断
,判断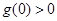 ,所以
,所以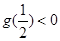 或
或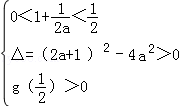 ,解得
,解得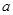 的取值范围;第二问,对
的取值范围;第二问,对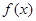 求导,令
求导,令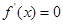 ,设出方程的两根,利用韦达定理得到两根之和、两根之积,判断导函数的正负,决定函数
,设出方程的两根,利用韦达定理得到两根之和、两根之积,判断导函数的正负,决定函数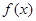 的单调性,求出最大值和最小值,代入求证的式子的左边,化简,得到
的单调性,求出最大值和最小值,代入求证的式子的左边,化简,得到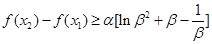 ,再求函数
,再求函数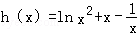 的最小值,通过不等式的传递性得到求证的表达式.
的最小值,通过不等式的传递性得到求证的表达式.试题解析:(I)由
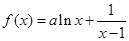 (
(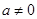 ),得:
),得: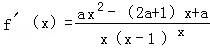 ,
,∵a≠0,令
 ,∴
,∴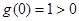 .
.令
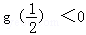 或
或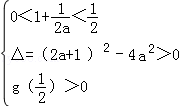 , 则
, 则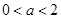 .
.(II)由(I)得:
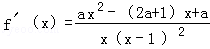 ,
,设
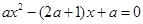 (
(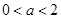 )的两根为
)的两根为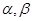 ,
,则
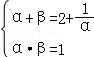 ,得
,得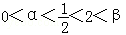 .
.当
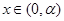 和
和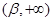 时,
时,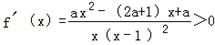 ,函数f(x)单调递增;
,函数f(x)单调递增;当
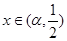 和
和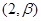 时,
时,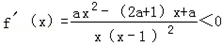 ,函数f(x)单调递减,
,函数f(x)单调递减,则
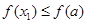 ,
,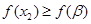 ,
,则
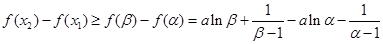
=
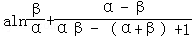 =
=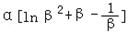 (利用
(利用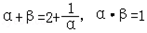 )
)令
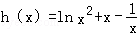 ,
,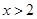 则
则 ,
,则函数
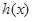 单调递增,
单调递增, 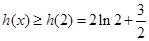 ,
,∴
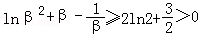 ,
,∵
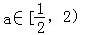 ,则
,则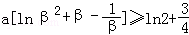 ,
,∴
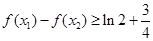 .
.
练习册系列答案
相关题目
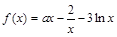 ,其中
,其中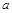 为常数.
为常数.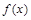 的图象在点
的图象在点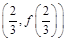 处的切线的斜率为1时,求函数
处的切线的斜率为1时,求函数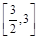 上的最小值;
上的最小值;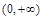 上既有极大值又有极小值,求实数
上既有极大值又有极小值,求实数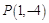 作函数
作函数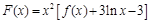 图象的切线,试问这样的切线有几条?并求这些切线的方程.
图象的切线,试问这样的切线有几条?并求这些切线的方程.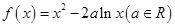 .
.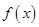 的单调区间;
的单调区间;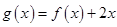 ,若
,若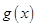 在
在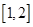 上单调递增,求
上单调递增,求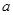 的取值范围.
的取值范围. 在(0,+
在(0,+ )内有定义,对于给定的正数K,定义函数
)内有定义,对于给定的正数K,定义函数 ,取函数
,取函数 ,恒有
,恒有 ,则
,则
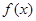 满足
满足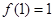 ,且
,且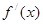 在R上恒有
在R上恒有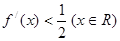 ,则不等式
,则不等式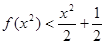 的解集是( )
的解集是( )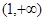
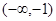
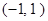
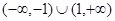
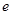 是自然对数的底数,若函数
是自然对数的底数,若函数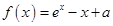 的图象始终在
的图象始终在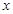 轴的上方,则实数
轴的上方,则实数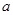 的取值范围 .
的取值范围 .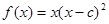 在
在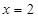 处有极大值,则常数
处有极大值,则常数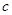 的值为________.
的值为________.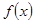 =
=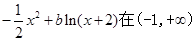 上是减函数,则
上是减函数,则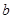 的取值范围是___________.
的取值范围是___________.