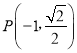题目内容
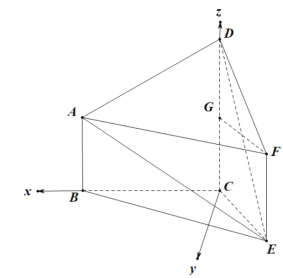
【题目】如图,在五面体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
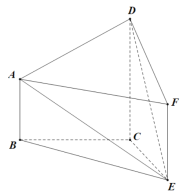
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据平行的传递性可得![]() ,再取
,再取![]() 中点为
中点为![]() ,连接
,连接![]() ,进而可得四边形
,进而可得四边形![]() 为平行四边形,再根据勾股定理证明
为平行四边形,再根据勾股定理证明![]() ,进而得到
,进而得到![]() 平面
平面![]() .
.
(2) 以点![]() 为坐标原点,分别以
为坐标原点,分别以![]() 、
、![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系![]() ,再分别求解平面
,再分别求解平面![]() 的法向量与平面
的法向量与平面![]() 的法向量,进而求得二面角的余弦值即可.
的法向量,进而求得二面角的余弦值即可.
(1)证明:因为![]() ,
,![]() ,
,
所以![]() .
.
取![]() 中点为
中点为![]() ,连接
,连接![]() ,所以
,所以![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() 且
且![]() ,
,
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,且
,且![]() .
.
因为![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
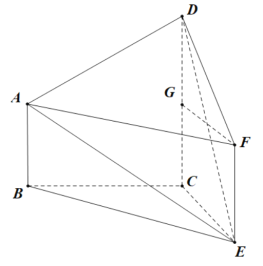
(2)由(1)知,![]() 平面
平面![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
故以点![]() 为坐标原点,分别以
为坐标原点,分别以![]() 、
、![]() 的方向为
的方向为![]() 轴、
轴、
![]() 轴的正方向,建立如图所示的空间直角坐标系
轴的正方向,建立如图所示的空间直角坐标系![]() .
.
所以![]()
所以![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则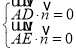 ,
,
所以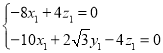 ,
,
取![]() ,则
,则![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,因为
,因为![]() ,
,
所以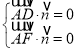 ,
,
所以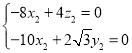 ,
,
取![]() ,则
,则![]() ,
,
所以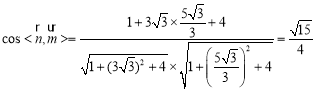 ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】光伏发电是利用太阳能电池及相关设备将太阳光能直接转化为电能.近几年在国内出台的光伏发电补贴政策的引导下,某地光伏发电装机量急剧上涨,如下表:
年份 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
新增光伏装机量 | 0.4 | 0.8 | 1.6 | 3.1 | 5.1 | 7.1 | 9.7 | 12.2 |
某位同学分别用两种模型:①![]() ,②
,②![]() 进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差等于
进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差等于![]() ):
):

经过计算得![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() .
.
(1)根据残差图,比较模型①,②的拟合效果,应该选择哪个模型?并简要说明理由.
(2)根据(1)的判断结果及表中数据建立![]() 关于
关于![]() 的回归方程,并预测该地区2020年新增光伏装机量是多少.(在计算回归系数时精确到0.01)
的回归方程,并预测该地区2020年新增光伏装机量是多少.(在计算回归系数时精确到0.01)
附:回归直线的斜率和截距的最小二乘估计公式分别为: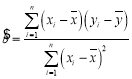 ,
,![]() .
.