题目内容
14. 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$. (1)求证:CD⊥平面PAC;
(2)如果如果N是棱AB上一点,且直线CN与平面MAB所成角的正弦值为$\frac{{\sqrt{10}}}{5}$,求$\frac{AN}{NB}$的值.
分析 (1)连结AC,由勾股定理得AB⊥AC,从而AC⊥CD,由线面垂直得PA⊥CD,由此能证明CD⊥平面PAC.
(2)以A为原点,AB,AC,AP所在直线分别为x,y,z轴,建立空间直角坐标系,由直线CN与平面MAB所成角的正弦值为$\frac{{\sqrt{10}}}{5}$,利用向量法能求出$\frac{AN}{NB}$的值.
解答  (1)证明:连结AC.因为在△ABC中,AB=AC=2,$BC=2\sqrt{2}$,
(1)证明:连结AC.因为在△ABC中,AB=AC=2,$BC=2\sqrt{2}$,
所以AB2+AC2=BC2,所以AB⊥AC.
因为AB∥CD,所以AC⊥CD.
又因为PA⊥底面ABCD,所以PA⊥CD.
因为AC∩PA=A,
所以CD⊥平面PAC.(4分)
(2)解:如图,以A为原点,AB,AC,AP所在直线分别为x,y,z轴,建立空间直角坐标系.
则A(0,0,0),P(0,0,2),B(2,0,0),C(0,2,0),D(-2,2,0),因为M是棱PD的中点,所以M(-1,1,1).
所以$\overrightarrow{AM}=(-1,1,1),\overrightarrow{AB}=(2,0,0)$,
设$\overrightarrow{n}$=(x,y,z)为平面MAB的法向量,
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AM}=-x+y+z=0}\\{\overrightarrow{n}•\overrightarrow{AB}=2x=0}\end{array}\right.$,
令y=1,得平面MAB的法向量$\overrightarrow{n}$=(0,1,-1),
因为N是在棱AB上一点,所以设N(x,0,0),$\overrightarrow{NC}$=(-x,2,0).
因为直线CN与平面MAB所成角的正弦值为$\frac{{\sqrt{10}}}{5}$,
设直线CN与平面MAB所成角为α,
则sinα=|cos<$\overrightarrow{NC},\overrightarrow{n}$>|=$\frac{|\overrightarrow{NC}•\overrightarrow{n}|}{|\overrightarrow{NC}|•|\overrightarrow{n}|}$=$\frac{2}{\sqrt{2}×\sqrt{{x}^{2}+4}}$=$\frac{\sqrt{10}}{5}$,
解得x=1,即AN=1,NB=1,所以$\frac{AN}{NB}$=1.
点评 本题考查向面垂直的证明,考查满足条件的线段的比值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案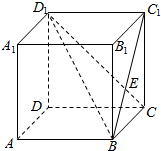 如图,正方体ABCD-A1B1C1D1中,则直线D1C与平面ABC所成角的大小等于( )
如图,正方体ABCD-A1B1C1D1中,则直线D1C与平面ABC所成角的大小等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
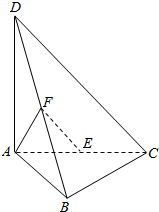 四面体ABCD中,AD⊥平面ABC,AB⊥BC,E,F分别为AC,BD的中点,AB=AD=2,∠BAC=60°.
四面体ABCD中,AD⊥平面ABC,AB⊥BC,E,F分别为AC,BD的中点,AB=AD=2,∠BAC=60°.