题目内容
用反证法证明命题“如果a＞b，那么
＞
”时，应假设
≤
≤
．
| 3 | a |
| 3 | b |
| 3 | a |
| 3 | b |
| 3 | a |
| 3 | b |
分析：根据要证结论的否定为
≤
，得到结论．
| 3 | a |
| 3 | b |
解答：解：由于
＞
的否定为：“
≤
”，
根据用反证法证明命题的方法，应先假设要证结论的否定成立，
故应假设：
≤
，
故答案为：
≤
．
| 3 | a |
| 3 | b |
| 3 | a |
| 3 | b |
根据用反证法证明命题的方法，应先假设要证结论的否定成立，
故应假设：
| 3 | a |
| 3 | b |
故答案为：
| 3 | a |
| 3 | b |
点评：本题考查用反证法证明数学命题，把要证的结论进行否定，得到要证的结论的反面，是解题的突破口．
练习册系列答案
相关题目
用反证法证明命题“如果a＞b，那么
＞
”时，假设的内容是（ ）
| 3 | a |
| 3 | b |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
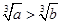”时，假设的内容应是 ( )
B．