题目内容
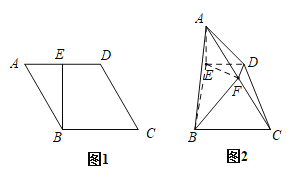
【题目】如图,三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() .以
.以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,连接
,连接![]() 和
和![]() .
.
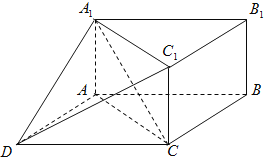
(1)求证:![]() 平面
平面![]() ;
;
(2)若二面角![]() 为45°,
为45°,
①证明:平面![]() 平面
平面![]() ;
;
②求直线![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.
【答案】(1)详见解析;(2)①详见解析;②![]() .
.
【解析】
(1)连接![]() ,证明
,证明![]() ,再利用线面平行的判定定理证明.
,再利用线面平行的判定定理证明.
(2)①取CD的中点O,连接![]() ,易证
,易证![]() 为二面角
为二面角![]() 的平面角,得到
的平面角,得到![]() ,结合
,结合![]() 平面
平面![]() ,得到
,得到![]() ,从而得到
,从而得到![]() 平面
平面![]() ,再利用
,再利用![]() ,由面面垂直的判定定理证明,②过A作
,由面面垂直的判定定理证明,②过A作![]() ,根据平面
,根据平面![]() 平面
平面![]() ,得到
,得到![]() 平面
平面![]() ,可知
,可知![]() 是直线
是直线![]() 与平面
与平面![]() 所成角,然后在
所成角,然后在![]() 中求解.
中求解.
(1)如图所示
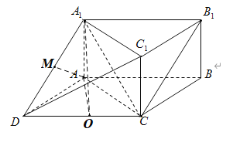
连接![]() ,在平行四边形ABCD中,
,在平行四边形ABCD中,![]() ,
,
在三棱柱![]() 中,又
中,又![]() ,
,
所以![]() ,
,
所以四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2)①取CD的中点O,连接![]() ,因为
,因为![]() ,
,
所以![]() ,又因为
,又因为![]() 平面
平面![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() ,
,
所以![]() 为二面角
为二面角![]() 的平面角,
的平面角,
在![]() 中,
中,![]() ,
,![]() ,
,
所以![]() ,又因为
,又因为![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ;
;
②过A作![]() ,因为平面
,因为平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() 是
是![]() 在平面
在平面![]() 上的射影,
上的射影,
所以![]() 是直线
是直线![]() 与平面
与平面![]() 所成角,
所成角,
在![]() 中,
中,![]() ,
,
![]() .
.

【题目】在2019年高考数学的全国Ⅲ卷中,文科和理科的选做题题目完全相同,第22题考查选修4-4:极坐标和参数方程;第23题考查选修4-5:不等式选讲.某校高三质量检测的命题采用了全国Ⅲ卷的形式,在测试结束后,该校数学组教师对该校全体高三学生的选做题得分情况进行了统计,得到两题得分的![]() 列联表如下(已知每名学生只做了一道题):
列联表如下(已知每名学生只做了一道题):
选做22题 | 选做23题 | 合计 | |
文科人数 | 50 | 60 | |
理科人数 | 40 | ||
总计 | 400 |
(1)完善![]() 列联表中的数据,判断能否有
列联表中的数据,判断能否有![]() 的把握认为“选做题的选择”与“文、理科的科类”有关;
的把握认为“选做题的选择”与“文、理科的科类”有关;
(2)经统计,第23题得分为0的学生中,理科生占理科总人数的![]() ,文科生占文科总人数的
,文科生占文科总人数的![]() ,在按分层抽样的方法在第23题得分为0的学生中随机抽取6名进行单独辅导,并在辅导后随机抽取2名学生进行测试,求被抽中进行测试的2名学生均为理科生的概率.
,在按分层抽样的方法在第23题得分为0的学生中随机抽取6名进行单独辅导,并在辅导后随机抽取2名学生进行测试,求被抽中进行测试的2名学生均为理科生的概率.
附: ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |