题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)讨论函数![]() 的单调性;
的单调性;
(3)若关于x的不等式![]() 恒成立,且k的最小值是m,求证:
恒成立,且k的最小值是m,求证:![]() .
.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 在
在![]() 为增函数,无减区间;
为增函数,无减区间;
当![]() 时,
时,![]() 在
在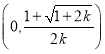 为增函数,在
为增函数,在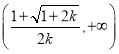 为减函数;(3)见解析.
为减函数;(3)见解析.
【解析】
(1)求出![]() 后可得曲线
后可得曲线![]() 在
在![]() 处的切线方程.
处的切线方程.
(2)就![]() 、
、![]() 时分别讨论函数
时分别讨论函数![]() 的符号后可得
的符号后可得![]() 的单调性.
的单调性.
(3)根据(2)中的结论可得![]() ,其中
,其中![]() 满足
满足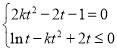 ,消去
,消去![]() 得到
得到![]() ,再利用导数可得
,再利用导数可得![]() 为增函数且存在唯一零点,故此不等式的解为
为增函数且存在唯一零点,故此不等式的解为![]() ,由此可得
,由此可得![]() ,利用分析法结合
,利用分析法结合![]() 的范围可证
的范围可证![]() .
.
(1)当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,所以曲线
,所以曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,
,
而![]() ,故切线方程为
,故切线方程为![]() .
.
(2)![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 为增函数,无减区间.
为增函数,无减区间.
当![]() 时,令
时,令![]() ,解得
,解得![]() 或
或![]() (舍)
(舍)
当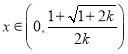 时,
时,![]() ,故
,故![]() 在
在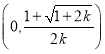 为增函数;
为增函数;
当 时,
时,![]() ,故
,故![]() 在
在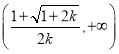 为减函数;
为减函数;
综上,当![]() 时,
时,![]() 在
在![]() 为增函数,无减区间;
为增函数,无减区间;
当![]() 时,
时,![]() 在
在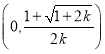 为增函数,在
为增函数,在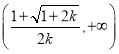 为减函数.
为减函数.
(3)由(2)可知,当![]() ,
,![]() 在
在![]() 为增函数,
为增函数,
因为![]() ,与题设矛盾,舍.
,与题设矛盾,舍.
当![]() 时,
时,![]() 在
在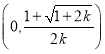 为增函数,在
为增函数,在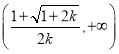 为减函数,
为减函数,
所以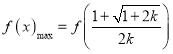 ,因为不等式
,因为不等式![]() 恒成立,故
恒成立,故![]() .
.
令![]() ,则
,则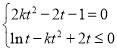 .
.
消去![]() ,则有
,则有![]() 即
即![]() ,
,
令![]() ,
,![]() ,则
,则![]() ,故
,故![]() 为
为![]() 上的增函数.
上的增函数.
又![]() ,
,![]() ,
,
因为![]() ,故
,故![]() ,故
,故![]() .
.
所以![]() 在
在![]() 上有且只有一个零点,设
上有且只有一个零点,设![]() 为
为![]() 的零点,
的零点,
故不等式![]() 的解为
的解为![]() 且
且![]() .
.
又![]() ,因为函数
,因为函数![]() 在
在![]() 为减函数,
为减函数,
故当![]() 时,
时,![]() 即
即![]() ,也就是
,也就是![]() .
.
要证![]() ,即证
,即证![]() ,
,
即证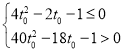 ,也就是证明
,也就是证明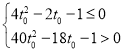 ,
,
即证![]() .
.
因为![]() ,而
,而![]() ,
,
故![]() 成立,所以
成立,所以![]() 成立.
成立.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某人某天的工作是驾车从![]() 地出发,到
地出发,到![]() 两地办事,最后返回
两地办事,最后返回![]() 地,
地,![]() ,三地之间各路段行驶时间及拥堵概率如下表
,三地之间各路段行驶时间及拥堵概率如下表
路段 | 正常行驶所用时间(小时) | 上午拥堵概率 | 下午拥堵概率 |
| 1 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到拥堵,则在该路段行驶时间需要延长1小时.
现有如下两个方案:
方案甲:上午从![]() 地出发到
地出发到![]() 地办事然后到达
地办事然后到达![]() 地,下午从
地,下午从![]() 地办事后返回
地办事后返回![]() 地;
地;
方案乙:上午从![]() 地出发到
地出发到![]() 地办事,下午从
地办事,下午从![]() 地出发到达
地出发到达![]() 地,办完事后返回
地,办完事后返回![]() 地.
地.
(1)若此人早上8点从![]() 地出发,在各地办事及午餐的累积时间为2小时,且采用方案甲,求他当日18点或18点之前能返回
地出发,在各地办事及午餐的累积时间为2小时,且采用方案甲,求他当日18点或18点之前能返回![]() 地的概率.
地的概率.
(2)甲乙两个方案中,哪个方案有利于办完事后更早返回![]() 地?请说明理由.
地?请说明理由.