题目内容
10.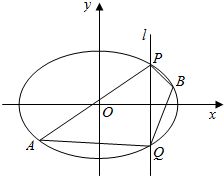 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,长轴长为4$\sqrt{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,长轴长为4$\sqrt{2}$.(1)求椭圆C的方程;
(2)直线l:x=2与椭圆C交于两点P、Q,其中P在第一象限,A、B是椭圆上位于直线l两侧的两个动点,满足∠APQ=∠BPQ,试问直线AB的斜率是否为定值?请说明理由.
分析 (1)通过题意直接计算即可;
(2)通过在椭圆C的方程$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1中令x=2可得P(2,1)、Q(2,-1),设A(x1,y1),B(x2,y2),利用∠APQ=∠BPQ,分别联立直线PA、PB与椭圆方程,结合韦达定理,直接计算$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$即可.
解答 解:(1)依题意:e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,2a=4$\sqrt{2}$,
∴a=2$\sqrt{2}$,c=$\sqrt{6}$,
∴b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{2}$,
∴椭圆C的方程为:$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1;
(2)结论:直线AB的斜率为定值$\frac{1}{2}$.
理由如下:
在椭圆C的方程$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1中令x=2,得y=±1,
∴P(2,1),Q(2,-1),
∵∠APQ=∠BPQ,∴直线PA的倾斜角与直线PB的倾斜角互补,
直线PA的斜率显然存在.
设直线PA的斜率为k,则直线PB的斜率为-k,
设A(x1,y1),B(x2,y2),
直线PA的方程为:y-1=k(x-2),即y=kx-2k+1,
联立$\left\{\begin{array}{l}{y=kx-2k+1}\\{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,消去y整理得:(1+4k2)x2+8k(1-2k)x+16k2-16k-4=0,
∵2、x1是该方程的两个实根,
∴2x1=$\frac{16{k}^{2}-16k-4}{1+4{k}^{2}}$,∴x1=$\frac{8{k}^{2}-8k-2}{1+4{k}^{2}}$,
同理,直线PB的方程为:y=-kx+2k+1,且x2=$\frac{8{k}^{2}+8k-2}{1+4{k}^{2}}$,
∴x1+x2=$\frac{16{k}^{2}-4}{1+4{k}^{2}}$,x1-x2=-$\frac{16k}{1+4{k}^{2}}$,
∴直线AB的斜率为:$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{(k{x}_{1}-2k+1)-(-k{x}_{2}+2k+1)}{{{x}_{1}-x}_{2}}$
=$\frac{k({x}_{1}+{x}_{2})-4k}{{x}_{1}-{x}_{2}}$
=$\frac{\frac{16{k}^{3}-4k}{1+4{k}^{2}}-4k}{-\frac{16k}{1+4{k}^{2}}}$
=$\frac{-8k}{-16k}$
=$\frac{1}{2}$.
点评 本题是一道直线与圆锥曲线的综合题,考查求椭圆的方程,考查运算求解能力,注意解题方法的积累,属于中档题.

| A. | 1 | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
| A. | (-∞,2$\sqrt{2}$) | B. | (2$\sqrt{2}$,+∞) | C. | (-∞,2) | D. | (2,+∞) |
| A. | -1-i | B. | 1+i | C. | 1-i | D. | -1+i |
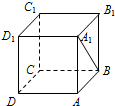
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |