题目内容
已知三次函数f(x)的导函数为f′(x),且f′(1)=0,f′(2)=3,f′(3)=12.(1)求f(x)-f(0)的表达式;
(2)若对任意的x∈[-1,4],都有f(x)>f′(x)成立,求f(0)的取值范围.
解:(1)设f(x)=ax3+bx2+cx+d,则f′(x)=3ax2+2bx+c.
∴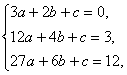 即
即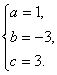
∴f(x)-f(0)=x3-3x2+3x.
(2)f′(x)=3x2-6x+3.对任意的x∈[-1,4],f(x)>f′(x)![]() f(x)-f′(x)=x3-?6x2+9x+f(0)-3>0
f(x)-f′(x)=x3-?6x2+9x+f(0)-3>0![]() f(0)>F(x)=-x3+6x2-9x+3.
f(0)>F(x)=-x3+6x2-9x+3.
∵F′(x)=-3x2+12x-9,
当x∈?[-1,?1)时,F′(x)<0;
当x=1或3时,F′(x)=0,当x∈(1,3)时,F′(x)>0;
当x∈(3,4]时,F′(x)<0,又F(-1)>F(3),F(-1)>F(1),F(-1)>F(4).
∴F(x)在[-1,4]上的最大值为F(-1)=19,f(0)的取值范围是(19,+∞).

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目