题目内容
已知函数 的定义域为
的定义域为 ,且同时满足下列条件:
,且同时满足下列条件:
(1) 是奇函数;
是奇函数;
(2) 在定义域上单调递减;
在定义域上单调递减;
(3) 求
求 的取值范围。
的取值范围。
【答案】

【解析】本题以抽象函数为例,在已知函数的单调性和奇偶性的前提下,解关于x的不等式,着重考查了函数的定义域和函数的简单性质等知识点,属于基础题.根据函数f(x)的定义域为(-7,7),原不等式的自变量应该在这个范围内,由此得-1<a<6.又因为f(x)是奇函数,且在定义域上单调递减,所以原不等式转化为1-a>1-a2,解之得a>4,结合前面求出的大前提,取交集可得实数a的取值范围.
解: ,则
,则 ,
,



练习册系列答案
相关题目
已知函数 的定义域为
的定义域为 ,部分对应值如下表。
,部分对应值如下表。 的导函数
的导函数 的图像如图所示。
的图像如图所示。
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|

下列关于函数 的命题:
的命题:
①函数 在
在 上是减函数;②如果当
上是减函数;②如果当 时,
时, 最大值是
最大值是 ,那么
,那么 的最大值为
的最大值为 ;③函数
;③函数 有
有 个零点,则
个零点,则 ;④已知
;④已知 是
是 的一个单调递减区间,则
的一个单调递减区间,则 的最大值为
的最大值为 。
。
其中真命题的个数是( )
A、4个 B、3个 C、2个 D、1个
 的定义域为
的定义域为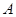 ,
,  ,且
,且 的真子集,求实数
的真子集,求实数 的取值范围.
的取值范围.




 的定义域为
的定义域为 ,且
,且 ,
, 为
为 ,
, 满足
满足 ,则
,则 的取值范围是
的取值范围是
 B.
B. C.
C. D.
D.