题目内容
(1)求(x2-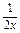 )9的展开式中的常数项;
)9的展开式中的常数项;
(2)已知(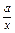 -
-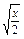 )9的展开式中x3的系数为
)9的展开式中x3的系数为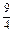 ,求常数a的值;
,求常数a的值;
(3)求(x2+3x+2)5的展开式中含x的项.
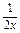 )9的展开式中的常数项;
)9的展开式中的常数项;(2)已知(
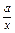 -
-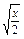 )9的展开式中x3的系数为
)9的展开式中x3的系数为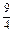 ,求常数a的值;
,求常数a的值;(3)求(x2+3x+2)5的展开式中含x的项.
(1) 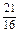 (2) a=4 (3) 含x的项为C
(2) a=4 (3) 含x的项为C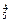 ·x·C
·x·C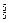 ·25+C
·25+C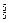 ·1·C
·1·C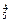 ·x·24=240x
·x·24=240x
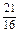 (2) a=4 (3) 含x的项为C
(2) a=4 (3) 含x的项为C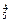 ·x·C
·x·C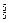 ·25+C
·25+C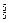 ·1·C
·1·C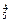 ·x·24=240x
·x·24=240x(1)设第r+1项为常数项,则
Tr+1=C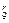 (x2)9-r·(-
(x2)9-r·(-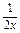 )r=(-
)r=(-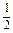 )rC
)rC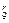 x
x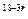
令18-3r=0,得r=6,即第7项为常数项.
T7=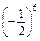 C
C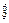 =
=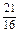 .
.
∴常数项为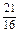 .
.
(2)设第r+1项是含x3的项,则有
C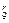 (
(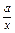 )9-r
)9-r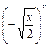 =
=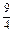 x3,得:xr-9x
x3,得:xr-9x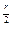 =x3,
=x3,
故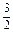 r-9=3,即r=8.
r-9=3,即r=8.
∴C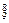 a(-
a(-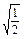 )8=
)8=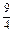 ,∴a=4.
,∴a=4.
(3)∵(x2+3x+2)5=(x+1)5(x+2)5,
(x2+3x+2)5的展开式中含x的项是(x+1)5展开式中的一次项与(x+2)5展开式中的常数项之积,(x+1)5展开式中的常数项与(x+2)5展开式中的一次项之积的代数和.
∴含x的项为C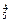 ·x·C
·x·C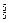 ·25+C
·25+C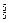 ·1·C
·1·C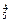 ·x·24=240x.
·x·24=240x.
Tr+1=C
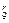 (x2)9-r·(-
(x2)9-r·(-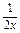 )r=(-
)r=(-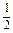 )rC
)rC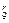 x
x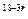
令18-3r=0,得r=6,即第7项为常数项.
T7=
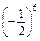 C
C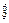 =
=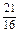 .
.∴常数项为
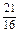 .
.(2)设第r+1项是含x3的项,则有
C
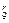 (
(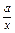 )9-r
)9-r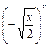 =
=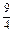 x3,得:xr-9x
x3,得:xr-9x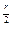 =x3,
=x3,故
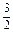 r-9=3,即r=8.
r-9=3,即r=8.∴C
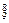 a(-
a(-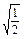 )8=
)8=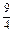 ,∴a=4.
,∴a=4.(3)∵(x2+3x+2)5=(x+1)5(x+2)5,
(x2+3x+2)5的展开式中含x的项是(x+1)5展开式中的一次项与(x+2)5展开式中的常数项之积,(x+1)5展开式中的常数项与(x+2)5展开式中的一次项之积的代数和.
∴含x的项为C
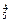 ·x·C
·x·C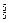 ·25+C
·25+C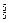 ·1·C
·1·C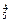 ·x·24=240x.
·x·24=240x.
练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
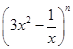 的展开式中各项系数的和是512,则展开式中的常数项为
的展开式中各项系数的和是512,则展开式中的常数项为 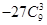
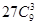
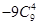
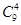
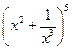 的展开式中常数项为 ;各项系数之和为 。(用数字作答)
的展开式中常数项为 ;各项系数之和为 。(用数字作答)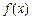 是定义在
是定义在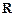 上的函数,且
上的函数,且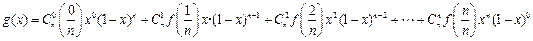 .
.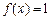 ,求
,求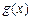 ;
;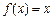 ,求
,求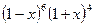 的展开式中
的展开式中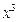 的系数.
的系数. ,则
,则 ( )
( )
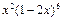 的展开式中,x5的系数为 .
的展开式中,x5的系数为 .