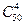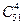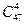题目内容
在（3x-2y）20的展开式中，求：
（1）二项式系数最大的项；
（2）系数绝对值最大的项；
（3）系数最大的项.
（1）二项式系数最大的项；
（2）系数绝对值最大的项；
（3）系数最大的项.
(1) C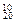
610x10y10 (2) T9=C
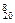312·28·x12y8是系数绝对值最大的项 (3)T9=C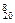·312·28·x12y8
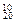610x10y10 (2) T9=C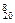312·28·x12y8是系数绝对值最大的项 (3)T9=C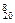·312·28·x12y8（1）二项式系数最大的项是第11项，
T11=C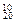310（-2）10x10y10=C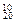610x10y10.
（2）设系数绝对值最大的项是第r+1项，
于是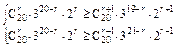
，
化简得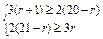
，解得7
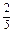≤r≤8.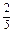
所以r=8,
即T9=C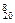312·28·x12y8是系数绝对值最大的项.
（3）由于系数为正的项为奇数项，故可设第2r-1项系数最大，于是
，
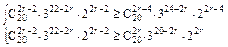化简得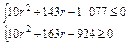
.
解之得r=5,即2×5-1=9项系数最大.
T9=C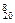·312·28·x12y8.
T11=C
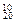310（-2）10x10y10=C610x10y10.（2）设系数绝对值最大的项是第r+1项，
于是
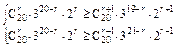，化简得
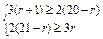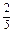，解得7≤r≤8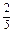.所以r=8,
即T9=C
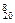312·28·x12y8是系数绝对值最大的项.（3）由于系数为正的项为奇数项，故可设第2r-1项系数最大，于是
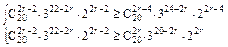，化简得
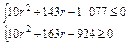.解之得r=5,即2×5-1=9项系数最大.
T9=C
·312·28·x12y8.
练习册系列答案
相关题目
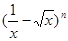的展开式中只有第四项的二项式系数最大，则展开式中的常数项等于（ ）
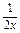)9的展开式中的常数项；
-
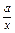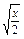)9的展开式中x3的系数为
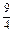，求常数a的值；
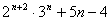能被25整除。
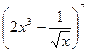的展开式中常数项是( )
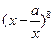的展开式中常数项为1120．
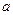的值；
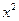的项．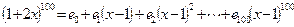
，
……，
.
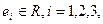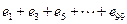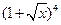的展开式中，
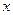的系数为 (用数字作答)。
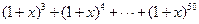展开式中，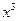
的系数是（ ）．
