题目内容
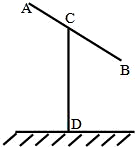 某建筑工地上所用的金属支架由AB与CD组成,如图所示,根据要求,AB至少长2a(a>2)m,C为AB中点,B到D的距离比CD的长小1m.∠BCD=60°.已知金属支架的材料每米的价格为10元.
某建筑工地上所用的金属支架由AB与CD组成,如图所示,根据要求,AB至少长2a(a>2)m,C为AB中点,B到D的距离比CD的长小1m.∠BCD=60°.已知金属支架的材料每米的价格为10元.
(1)设AB=2x,CD=y,试用x表示y;
(2)怎样设计AB、CD的长,可使建造这个支架的成本最低?
解:(1)如图,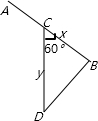 由余弦定理得:BD2=x2+y2-2xycos60°,∴BD=
由余弦定理得:BD2=x2+y2-2xycos60°,∴BD= ;
;
由题意知,BD=CD-1,即 =y-1,∴y=
=y-1,∴y=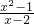 (其中x≥a>2);
(其中x≥a>2);
(2)设支架的造价为:W=10(2x+y),不妨令z=2x+y=2x+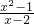 ,
,
如果设t=x-2,那么t≥a-2>0,∴z=2(t+2)+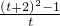 =3(t+
=3(t+ )+8;
)+8;
当a-2>1,即a>3时,∵z=3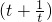 +8在[a-2,+∞)上单调递增,∴x=a时,有AB=2a,CD=
+8在[a-2,+∞)上单调递增,∴x=a时,有AB=2a,CD= ,这时造价W的值最小;
,这时造价W的值最小;
当 2<a≤3时,t=1,x=3,这时造价W的值也最小,且有AB=6,CD=8.
分析:(1)△BCD中,BC=x,CD=y,∠BCD=60°,由余弦定理可求BD;又BD比CD小1,可得x,y的关系式;
(2)由造价函数:W=10(2x+y)=10(2x+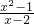 )(其中x≥a>2),不妨设t=x-2≥a-2>0,化简W为t的函数容易求出结果;
)(其中x≥a>2),不妨设t=x-2≥a-2>0,化简W为t的函数容易求出结果;
点评:本题借助三角形的余弦定理建立函数解析式,考查函数的最值问题,是中档题.
 由余弦定理得:BD2=x2+y2-2xycos60°,∴BD=
由余弦定理得:BD2=x2+y2-2xycos60°,∴BD= ;
;由题意知,BD=CD-1,即
 =y-1,∴y=
=y-1,∴y=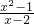 (其中x≥a>2);
(其中x≥a>2);(2)设支架的造价为:W=10(2x+y),不妨令z=2x+y=2x+
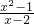 ,
,如果设t=x-2,那么t≥a-2>0,∴z=2(t+2)+
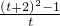 =3(t+
=3(t+ )+8;
)+8; 当a-2>1,即a>3时,∵z=3
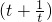 +8在[a-2,+∞)上单调递增,∴x=a时,有AB=2a,CD=
+8在[a-2,+∞)上单调递增,∴x=a时,有AB=2a,CD= ,这时造价W的值最小;
,这时造价W的值最小;当 2<a≤3时,t=1,x=3,这时造价W的值也最小,且有AB=6,CD=8.
分析:(1)△BCD中,BC=x,CD=y,∠BCD=60°,由余弦定理可求BD;又BD比CD小1,可得x,y的关系式;
(2)由造价函数:W=10(2x+y)=10(2x+
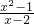 )(其中x≥a>2),不妨设t=x-2≥a-2>0,化简W为t的函数容易求出结果;
)(其中x≥a>2),不妨设t=x-2≥a-2>0,化简W为t的函数容易求出结果;点评:本题借助三角形的余弦定理建立函数解析式,考查函数的最值问题,是中档题.

练习册系列答案
相关题目
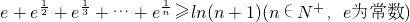 .
.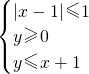 时,则t=x+y的最大值是
时,则t=x+y的最大值是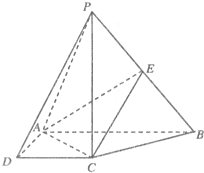 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点. ,求三棱锥C-ABE高的大小.
,求三棱锥C-ABE高的大小.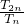 ,
,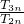 ,…为等比数列;
,…为等比数列; ∥
∥ ,且
,且 ,则
,则 的长度与向量
的长度与向量 的长度相等,且它们是始点、终点相反的向量
的长度相等,且它们是始点、终点相反的向量 是共线向量,则A、B、C、D四点共线
是共线向量,则A、B、C、D四点共线 ,E为CC1的中点,则直线AC1与平面BED的距离为
,E为CC1的中点,则直线AC1与平面BED的距离为