题目内容
已知正四棱柱ABCD-A1B1C1D1中,AB=2,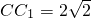 ,E为CC1的中点,则直线AC1与平面BED的距离为
,E为CC1的中点,则直线AC1与平面BED的距离为
- A.2
- B.

- C.

- D.1
D
分析:先利用线面平行的判定定理证明直线C1A∥平面BDE,再将线面距离转化为点面距离,最后利用等体积法求点面距离即可
解答:如图: 连接AC,交BD于O,在三角形CC1A中,易证OE∥C1A,从而C1A∥平面BDE,
连接AC,交BD于O,在三角形CC1A中,易证OE∥C1A,从而C1A∥平面BDE,
∴直线AC1与平面BED的距离即为点A到平面BED的距离,设为h,
在三棱锥E-ABD中,VE-ABD= S△ABD×EC=
S△ABD×EC= ×
× ×2×2×
×2×2× =
=
在三棱锥A-BDE中,BD=2 ,BE=
,BE= ,DE=
,DE= ,∴S△EBD=
,∴S△EBD= ×2
×2 ×
×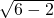 =2
=2
∴VA-BDE= ×S△EBD×h=
×S△EBD×h= ×2
×2 ×h=
×h=
∴h=1
故选 D
点评:本题主要考查了线面平行的判定,线面距离与点面距离的转化,三棱锥的体积计算方法,等体积法求点面距离的技巧,属基础题
分析:先利用线面平行的判定定理证明直线C1A∥平面BDE,再将线面距离转化为点面距离,最后利用等体积法求点面距离即可
解答:如图:
 连接AC,交BD于O,在三角形CC1A中,易证OE∥C1A,从而C1A∥平面BDE,
连接AC,交BD于O,在三角形CC1A中,易证OE∥C1A,从而C1A∥平面BDE,∴直线AC1与平面BED的距离即为点A到平面BED的距离,设为h,
在三棱锥E-ABD中,VE-ABD=
 S△ABD×EC=
S△ABD×EC= ×
× ×2×2×
×2×2× =
=
在三棱锥A-BDE中,BD=2
 ,BE=
,BE= ,DE=
,DE= ,∴S△EBD=
,∴S△EBD= ×2
×2 ×
×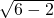 =2
=2
∴VA-BDE=
 ×S△EBD×h=
×S△EBD×h= ×2
×2 ×h=
×h=
∴h=1
故选 D
点评:本题主要考查了线面平行的判定,线面距离与点面距离的转化,三棱锥的体积计算方法,等体积法求点面距离的技巧,属基础题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,已知正四棱柱ABCD-A1B1C1D1的底面边长为1,点E在棱AA1上,A1C∥平面EBD,截面EBD的面积为
如图所示,已知正四棱柱ABCD-A1B1C1D1的底面边长为1,点E在棱AA1上,A1C∥平面EBD,截面EBD的面积为 如图,已知正四棱柱ABCD-A1B1C1D1与它的侧视图(或称左视图),E是DD1上一点,AE⊥B1C.
如图,已知正四棱柱ABCD-A1B1C1D1与它的侧视图(或称左视图),E是DD1上一点,AE⊥B1C. (2006•广州模拟)已知正四棱柱ABCD-A1B1C1D1,AB=BC=1,AA1=2,点E为CC1的中点,点F为BD1的中点.
(2006•广州模拟)已知正四棱柱ABCD-A1B1C1D1,AB=BC=1,AA1=2,点E为CC1的中点,点F为BD1的中点.