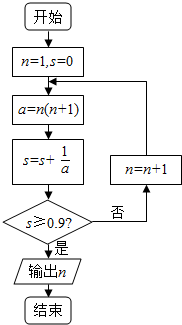
题目内容

2．函数y=2|1+x|的图象大致是（　　）
A．B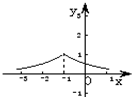．C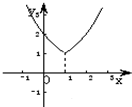．D．

分析 根据函数的对称性，单调性，值域即可判断．

解答 解：y=2|1+x|=$\left\{\begin{array}{l}{{2}^{1+x，x≥-1}}\\{{2}^{-1-x}，x＜-1}\end{array}\right.$，
则其图象关于x=-1对称，值域为（1，+∞），在（-∞，-1）上为减函数，在（-1，+∞）为增函数，
故选：A．

点评 本题考查了图象的识别，关键是掌握函数的对称性，单调性，值域，属于基础题．

练习册系列答案
相关题目
12．已知函数f（x）是R上的奇函数，且x＞0时，f（x）=-x2+2x．
（1）求f（x）的解析式；
（2）在如图的直角坐标系中画出函数求f（x）的图象，并求不等式f（x）＜0的解集．
13．已知a=log3650.99、b=1.01365、c=0.99365，则a、b、c的大小关系为（　　）
A．a＜c＜bB．b＜a＜cC．a＜b＜cD．b＜c＜a
10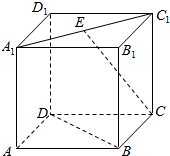．如图，在正方体ABCD-A1B1C1D1中，E为A1C1的中点，则异面直线CE与BD所成的角为（　　）
A．30°B．45°C．60°D．90°
17．（Ⅰ）已知a，b∈R+，求证：（a+b）（a2+b2）（a3+b3）≥8a3b3；
（Ⅱ）已知a、b、c∈R+，且a+b+c=1．求证：$（{\frac{1}{a}-1}）（{\frac{1}{b}-1}）（{\frac{1}{c}-1}）≥8$．
7．如图所示，程序框图（算法流程图）的输出结果为9．
14．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左右焦点F1、F2与椭圆短轴的一个端点构成边长为4的正三角形．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）已知过椭圆C上一点（x0，y0），与椭圆C相切的直线方程为$\frac{{{x_0}x}}{a^2}+\frac{{{y_0}y}}{b^2}$=1．过椭圆C上任意一点P作椭圆C的切线与直线F1P的垂线F1M相交于点M，求点M的轨迹方程；
（Ⅲ）若切线MP与直线x=-2交于点N，求证：$\frac{{|N{F_1}|}}{{|M{F_1}|}}$为定值．
11．（1）计算${27^{-\frac{1}{3}}}+lg0.01-ln\sqrt{e}+{3^{{{log}_3}2}}$
（2）已知x+x-1=3，求$\frac{{{x^{\frac{1}{2}}}+{x^{-\frac{1}{2}}}}}{{{x^2}-{x^{-2}}}}$的值．
12．若角α的终边过点（-1，2），则cos（π-2α）的值为（　　）
A．$\frac{3}{5}$B．-$\frac{3}{5}$C．$\frac{\sqrt{5}}{5}$D．-$\frac{\sqrt{5}}{5}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网