题目内容
如图,平面内的定点F到定直线l的距离为2,定点E满足:|
(1)建立适当的直角坐标系,求动点P的轨迹方程;
(2)若经过点E的直线l1与点P的轨迹交于相异两点A、B,令∠AFB=θ,当![]() 4π≤θ≤π时,求直线l1的斜率k的取值范围.
4π≤θ≤π时,求直线l1的斜率k的取值范围.
解:(1)以FG的中点为原点,以EF为y轴建立直角坐标系xOy.设P(x,y),
则F(0,1)、E(0,3),l:y=-1.
∵![]() ,
,![]() ,∴Q(x,-1),M(
,∴Q(x,-1),M(![]() ,0).
,0).
由![]() =0,∴(
=0,∴(![]() )·x+(-y)(-2)=0,
)·x+(-y)(-2)=0,
即所求点P的轨迹方程为x2=4y.
(2)设A(x1,y1),B(x2,y2)(x1≠x2),该直线l的方程为y=kx+3.
由 ,得x2-4kx-12=0,∴x1+x2=4k,x1·x2=-12.
,得x2-4kx-12=0,∴x1+x2=4k,x1·x2=-12.
∴y1·y2=![]() =9,y1+y2=k(x1+x2)+6=4k2+6,
=9,y1+y2=k(x1+x2)+6=4k2+6,
∵![]() =(x1,y1-1),
=(x1,y1-1),![]() =(x2,y2-1),
=(x2,y2-1),
∴![]() ·
·![]() =x1x2+y1y2-(y1+y2)+1=-4k2-8.
=x1x2+y1y2-(y1+y2)+1=-4k2-8.
而|![]() |·|
|·|![]() |=(y1+1)(y2+1)=y1·y2+(y1+y2)+1=4k2+16,
|=(y1+1)(y2+1)=y1·y2+(y1+y2)+1=4k2+16,
∴cosθ=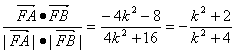 ,
,
∵![]() ≤θ≤π,-1≤cosθ≤
≤θ≤π,-1≤cosθ≤![]() ,
,
即-1≤![]() ,∴k2≥
,∴k2≥![]() .
.
解得k≥![]() 或k≤
或k≤![]() .
.
∴直线l1的斜率k≥![]() 或k≤
或k≤![]() .
.

练习册系列答案
相关题目
 (2006•海淀区二模)如图,平面内的定点F到定直线l的距离为2,定点E满足:|
(2006•海淀区二模)如图,平面内的定点F到定直线l的距离为2,定点E满足:|

 |=2且EF⊥l于G,点Q是直线l上一动点,点M满足
|=2且EF⊥l于G,点Q是直线l上一动点,点M满足 =0.
=0. π≤θ<π时,求直线l1的斜率k的取值范围.
π≤θ<π时,求直线l1的斜率k的取值范围.