题目内容
如图,平面内的定点F到定直线l的距离为2,定点E满足:| |=2且EF⊥l于G,点Q是直线l上一动点,点M满足
|=2且EF⊥l于G,点Q是直线l上一动点,点M满足 =0.
=0.(1)建立适当的直角坐标系,求动点P的轨迹方程;
(2)若经过点E的直线l1与点P的轨迹交于相异两点A、B,令∠AFB=θ,当
 π≤θ<π时,求直线l1的斜率k的取值范围.
π≤θ<π时,求直线l1的斜率k的取值范围.
【答案】分析:(1)以FG的中点O为原点,以EF所在直线为y轴,建立平面直角坐标系,设出动点P的坐标,求出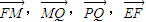 的坐标,由
的坐标,由 求出Q,M的坐标,由
求出Q,M的坐标,由 列式求出P点的轨迹;
列式求出P点的轨迹;
(2)设出直线l1 的方程,和抛物线方程联立后化为关于x的一元二次方程,利用根与系数关系得到两交点横坐标的和与积,进一步得到纵坐标的和与积,然后把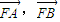 的数量积与模用含有k的代数式表示,代入向量夹角公式后可求值.
的数量积与模用含有k的代数式表示,代入向量夹角公式后可求值.
解答: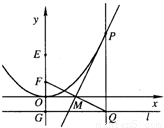 解:(1)以FG的中点O为原点,以EF所在直线为y轴,建立平面直角坐标系
解:(1)以FG的中点O为原点,以EF所在直线为y轴,建立平面直角坐标系
xoy,设点P(x,y),则F(0,1),E(0,3),l:y=-1
∵ ,∴
,∴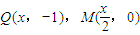
∵ ,∴
,∴ .
.
即所求点P轨迹方程x2=4y;
(2)设点A(x1,y1),B(x2,y2)(x1≠x2)
设直线l1的方程为y=kx+3(k≠0).
由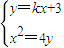 ,得x2-4kx-12=0
,得x2-4kx-12=0
∴x1+x2=4k,x1x2=-12
∴
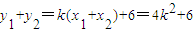
∵ ,
,
∴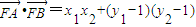
=x1x2+y1y2-(y1+y2)+1
=-12+9-4k2-6+1
=-4k2-8.
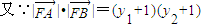
=
∴
由于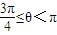 ,
,
∴ ,即
,即 .
.
∴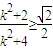 ,∴
,∴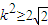 ,解得
,解得 或
或 .
.
∴直线l1 的斜率k的取值范围是{k| 或
或 }.
}.
点评:本题考查了直线的斜率,考查了与直线有关的动点轨迹方程问题,训练了平面向量在解题中的应用,利用根与系数关系解题是处理该题的关键,考查了学生的计算能力,是难题.
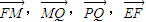 的坐标,由
的坐标,由 求出Q,M的坐标,由
求出Q,M的坐标,由 列式求出P点的轨迹;
列式求出P点的轨迹;(2)设出直线l1 的方程,和抛物线方程联立后化为关于x的一元二次方程,利用根与系数关系得到两交点横坐标的和与积,进一步得到纵坐标的和与积,然后把
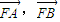 的数量积与模用含有k的代数式表示,代入向量夹角公式后可求值.
的数量积与模用含有k的代数式表示,代入向量夹角公式后可求值.解答:
 解:(1)以FG的中点O为原点,以EF所在直线为y轴,建立平面直角坐标系
解:(1)以FG的中点O为原点,以EF所在直线为y轴,建立平面直角坐标系xoy,设点P(x,y),则F(0,1),E(0,3),l:y=-1
∵
 ,∴
,∴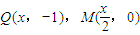
∵
 ,∴
,∴ .
.即所求点P轨迹方程x2=4y;
(2)设点A(x1,y1),B(x2,y2)(x1≠x2)
设直线l1的方程为y=kx+3(k≠0).
由
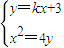 ,得x2-4kx-12=0
,得x2-4kx-12=0∴x1+x2=4k,x1x2=-12
∴

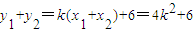
∵
 ,
,∴
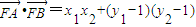
=x1x2+y1y2-(y1+y2)+1
=-12+9-4k2-6+1
=-4k2-8.
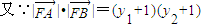
=

∴

由于
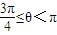 ,
,∴
 ,即
,即 .
.∴
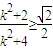 ,∴
,∴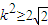 ,解得
,解得 或
或 .
.∴直线l1 的斜率k的取值范围是{k|
 或
或 }.
}.点评:本题考查了直线的斜率,考查了与直线有关的动点轨迹方程问题,训练了平面向量在解题中的应用,利用根与系数关系解题是处理该题的关键,考查了学生的计算能力,是难题.

练习册系列答案
相关题目
 (2006•海淀区二模)如图,平面内的定点F到定直线l的距离为2,定点E满足:|
(2006•海淀区二模)如图,平面内的定点F到定直线l的距离为2,定点E满足:|

