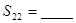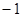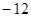题目内容
(本小题满分14分)数列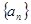 满足
满足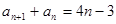
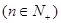 .
.
(Ⅰ)若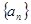 是等差数列,求其通项公式;
是等差数列,求其通项公式;
(Ⅱ)若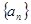 满足
满足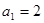 ,
,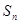 为
为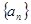 的前
的前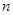 项和,求
项和,求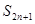 .
.
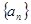 满足
满足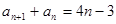
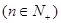 .
.(Ⅰ)若
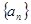 是等差数列,求其通项公式;
是等差数列,求其通项公式;(Ⅱ)若
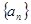 满足
满足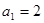 ,
,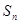 为
为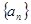 的前
的前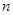 项和,求
项和,求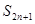 .
.解:(I)由题意得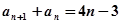 …①
…①  …②.
…②.
②-①得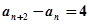 ,∵{
,∵{ }是等差数列,设公差为d,∴d=2, ………….4分
}是等差数列,设公差为d,∴d=2, ………….4分
∵ ∴
∴ ,∴
,∴  ,∴
,∴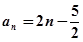 …….……….…7分
…….……….…7分
(Ⅱ)∵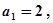
 ,∴
,∴ ….…………………….………8分
….…………………….………8分
又∵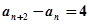 ,∴数列的奇数项与偶数项分别成等差数列,公差均为4
,∴数列的奇数项与偶数项分别成等差数列,公差均为4
∴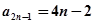 ,
,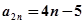 ….………………………….……….……………………11分
….………………………….……….……………………11分

= =
=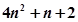 ….….……….……14分
….….……….……14分
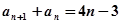 …①
…①  …②.
…②.②-①得
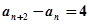 ,∵{
,∵{ }是等差数列,设公差为d,∴d=2, ………….4分
}是等差数列,设公差为d,∴d=2, ………….4分∵
 ∴
∴ ,∴
,∴  ,∴
,∴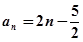 …….……….…7分
…….……….…7分(Ⅱ)∵
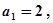
 ,∴
,∴ ….…………………….………8分
….…………………….………8分又∵
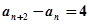 ,∴数列的奇数项与偶数项分别成等差数列,公差均为4
,∴数列的奇数项与偶数项分别成等差数列,公差均为4∴
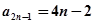 ,
,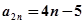 ….………………………….……….……………………11分
….………………………….……….……………………11分
=
 =
=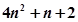 ….….……….……14分
….….……….……14分略

练习册系列答案
相关题目
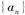 的前n项和为
的前n项和为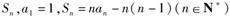 .
.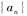 的通项公式;
的通项公式;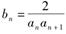 ,求数列
,求数列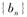 的前n项和Tn
的前n项和Tn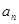 }满足
}满足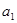 =1,
=1,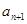 =
=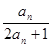 ,(1)计算
,(1)计算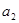 ,
,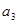 ,
,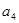 的值;
的值;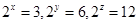 ,则x,y,z三个数依次成什么数列
,则x,y,z三个数依次成什么数列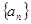 中,
中,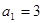 ,其前
,其前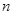 项和为
项和为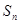 ,等比数列
,等比数列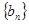 的各项均为正数,
的各项均为正数,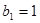 ,公比为
,公比为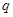 ,且
,且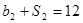 ,
, 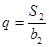 .(Ⅰ)求
.(Ⅰ)求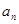 与
与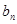 ;(Ⅱ)设数列
;(Ⅱ)设数列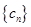 满足
满足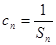 ,求
,求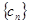 的前
的前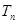
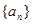 为递增数列,且
为递增数列,且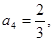
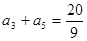 ,数列
,数列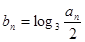 (n∈N※)
(n∈N※)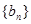 的前
的前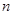 项和
项和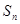 ;
;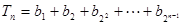 ,求使
,求使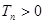 成立的最小值
成立的最小值 的前
的前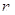 项和为
项和为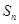 ,且满足
,且满足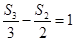 ,则数列
,则数列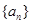 的公差是_________
的公差是_________ }中,
}中,
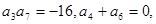 求{
求{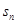 . .
. . 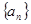 的前n项和为
的前n项和为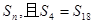 ,则
,则