题目内容
(本小题满分14分)
已知函数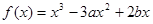 在点
在点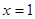 处有极小值-1,
处有极小值-1,
(1)求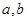 的值 (2)求出
的值 (2)求出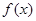 的单调区间.
的单调区间.
(3)求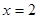 处的切线方程.
处的切线方程.
已知函数
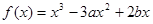 在点
在点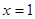 处有极小值-1,
处有极小值-1,(1)求
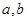 的值 (2)求出
的值 (2)求出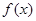 的单调区间.
的单调区间.(3)求
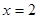 处的切线方程.
处的切线方程.(1)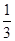 ,
,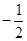 ;(2)
;(2)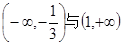 为函数
为函数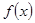 单调递增区间 ,
单调递增区间 ,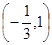 为函数
为函数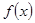 单调递减区间 ;(3)
单调递减区间 ;(3) 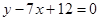 .
.
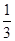 ,
,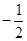 ;(2)
;(2)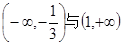 为函数
为函数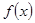 单调递增区间 ,
单调递增区间 ,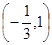 为函数
为函数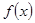 单调递减区间 ;(3)
单调递减区间 ;(3) 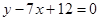 .
.第一问利用函数在x=1处有极小值-1,可知其导数为零,同时函数值为-1,联立方程组得到a,b的值。
第二问中,结合第一问的结论,递进关系,再确定导数,利用导数的正负,来判定函数的单调性。
解:(1)由已知得:
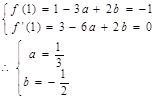 (2分)
(2分)
(4分)
(2)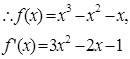 (6分)
(6分)
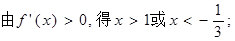
即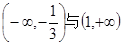 为函数
为函数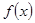 单调递增区间 (8分)
单调递增区间 (8分)
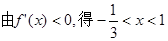
即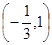 为函数
为函数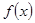 单调递减区间 (10分)
单调递减区间 (10分)
(3)
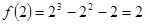 ,即过点
,即过点 (12分)
(12分)
 , (13分)
, (13分)
所以得:切线方程为: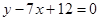 (14分)
(14分)
第二问中,结合第一问的结论,递进关系,再确定导数,利用导数的正负,来判定函数的单调性。
解:(1)由已知得:
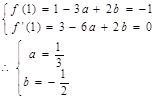 (2分)
(2分)(4分)
(2)
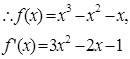 (6分)
(6分)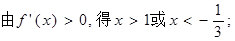
即
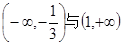 为函数
为函数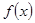 单调递增区间 (8分)
单调递增区间 (8分)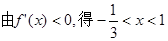
即
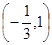 为函数
为函数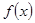 单调递减区间 (10分)
单调递减区间 (10分)(3)

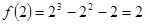 ,即过点
,即过点 (12分)
(12分) , (13分)
, (13分) 所以得:切线方程为:
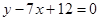 (14分)
(14分) 
练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
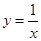 在点
在点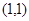 处的切线与直线
处的切线与直线 垂直,则
垂直,则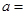 .
.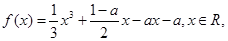 其中a>0.
其中a>0.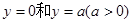 之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往. 家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读. 每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d, 0)处的学校.已知船速为
之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往. 家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读. 每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d, 0)处的学校.已知船速为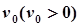 ,车速为
,车速为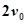 (水流速度忽略不计).若d=2a,求该学生早晨上学时,从家出发到达学校所用的最短时间.
(水流速度忽略不计).若d=2a,求该学生早晨上学时,从家出发到达学校所用的最短时间.
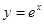 的切线,则切点坐标是________,切线斜率是_______.
的切线,则切点坐标是________,切线斜率是_______.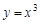 在点
在点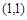 处的切线方程是 ;
处的切线方程是 ;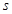 (单位:m)关于时间
(单位:m)关于时间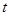 (单位:s)的函数为
(单位:s)的函数为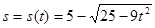 ,求当
,求当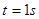 时,梯子上端下滑的速度为( )
时,梯子上端下滑的速度为( )



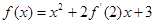 ,则
,则 .
.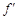 (-1)=4,则a的值等于________.
(-1)=4,则a的值等于________.